Материал из Википедии - свободной энциклопедии

Бесконечно малая - числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая - числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Исчисление бесконечно малых и больших

Исчисление бесконечно малых - вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений , составляющих основу современной высшей математики . Понятие бесконечно малой величины тесно связано с понятием предела .

Бесконечно малая

Последовательность $a\_n$ называется бесконечно малой , если $\backslash lim\backslash limits\_\{n\backslash to\backslash infty\}a\_n=0$. Например, последовательность чисел $a\_n=\backslash dfrac\{1\}\{n\}$ - бесконечно малая.

Функция называется бесконечно малой в окрестности точки $x\_0$, если $\backslash lim\backslash limits\_\{x\backslash to\; x\_0\}f(x)=0$.

Функция называется бесконечно малой на бесконечности , если $\backslash lim\backslash limits\_\{x\backslash to+\backslash infty\}f(x)=0$ либо $\backslash lim\backslash limits\_\{x\backslash to-\backslash infty\}f(x)=0$.

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если $\backslash lim\backslash limits\_\{x\backslash to+\backslash infty\}f(x)=a$, то $f(x)-a=\backslash alpha(x)$, $\backslash lim\backslash limits\_\{x\backslash to+\backslash infty\}(f(x)-a)=0$.

Подчеркнём, что бесконечно малую величину следует понимать как переменную величину (функцию), которая лишь в процессе своего изменения [при стремлении $x$ к $a$ (из $\backslash lim\backslash limits\_\{x\backslash to\; a\}f(x)=0$)] делается меньше произвольного числа ($\backslash varepsilon$). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.

Бесконечно большая

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция $x\backslash sin\; x$, неограниченная с обеих сторон, не является бесконечно большой при $x\backslash to+\backslash infty$.

Последовательность $a\_n$ называется бесконечно большой , если $\backslash lim\backslash limits\_\{n\backslash to\backslash infty\}a\_n=\backslash infty$.

Функция называется бесконечно большой в окрестности точки $x\_0$, если $\backslash lim\backslash limits\_\{x\backslash to\; x\_0\}f(x)=\backslash infty$.

Функция называется бесконечно большой на бесконечности , если $\backslash lim\backslash limits\_\{x\backslash to+\backslash infty\}f(x)=\backslash infty$ либо $\backslash lim\backslash limits\_\{x\backslash to-\backslash infty\}f(x)=\backslash infty$.

Как и в случае бесконечно малых, необходимо отметить, что ни одно отдельно взятое значение бесконечно большой величины не может быть названо как «бесконечно большое» - бесконечно большая величина - это функция , которая лишь в процессе своего изменения может стать больше произвольно взятого числа.

Свойства бесконечно малых

• Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
• Произведение бесконечно малых - бесконечно малая.
• Произведение бесконечно малой последовательности на ограниченную - бесконечно малая. Как следствие, произведение бесконечно малой на константу - бесконечно малая.
• Если $a\_n$ - бесконечно малая последовательность, сохраняющая знак, то $b\_n=\backslash dfrac\{1\}\{a\_n\}$ - бесконечно большая последовательность.

Сравнение бесконечно малых

Определения

Допустим, у нас есть бесконечно малые при одном и том же $x\backslash to\; a$ величины $\backslash alpha(x)$ и $\backslash beta(x)$ (либо, что не важно для определения, бесконечно малые последовательности).

• Если $\backslash lim\backslash limits\_\{x\backslash to\; a\}\backslash dfrac\{\backslash beta\}\{\backslash alpha\}=0$, то $\backslash beta$ - бесконечно малая высшего порядка малости , чем $\backslash alpha$. Обозначают $\backslash beta=o(\backslash alpha)$ или $\backslash beta\backslash prec\backslash alpha$.
• Если $\backslash lim\backslash limits\_\{x\backslash to\; a\}\backslash dfrac\{\backslash beta\}\{\backslash alpha\}=\backslash infty$, то $\backslash beta$ - бесконечно малая низшего порядка малости , чем $\backslash alpha$. Соответственно $\backslash alpha=o(\backslash beta)$ или $\backslash alpha\backslash prec\backslash beta$.
• Если $\backslash lim\backslash limits\_\{x\backslash to\; a\}\backslash dfrac\{\backslash beta\}\{\backslash alpha\}=c$ (предел конечен и не равен 0), то $\backslash alpha$ и $\backslash beta$ являются бесконечно малыми величинами одного порядка малости . Это обозначается как $\backslash alpha\backslash asymp\backslash beta$ или как одновременное выполнение отношений $\backslash beta=O(\backslash alpha)$ и $\backslash alpha=O(\backslash beta)$. Следует заметить, что в некоторых источниках можно встретить обозначение, когда одинаковость порядков записывают в виде только одного отношения «о большое», что является вольным использованием данного символа.
• Если $\backslash lim\backslash limits\_\{x\backslash to\; a\}\backslash dfrac\{\backslash beta\}\{\backslash alpha^m\}=c$ (предел конечен и не равен 0), то бесконечно малая величина $\backslash beta$ имеет $m$-й порядок малости относительно бесконечно малой $\backslash alpha$.

Для вычисления подобных пределов удобно использовать правило Лопиталя .

Примеры сравнения

• При $\{x\backslash to\; 0\}$ величина $x^5$ имеет высший порядок малости относительно $x^3$, так как $\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{x^5\}\{x^3\}=0$. С другой стороны, $x^3$ имеет низший порядок малости относительно $x^5$, так как $\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{x^3\}\{x^5\}=\backslash infty$.

С использованием О -символики полученные результаты могут быть записаны в следующем виде $x^5=o(x^3)$.

• $\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{2x^2+6x\}\{x\}=\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{2x+6\}\{1\}=\backslash lim\backslash limits\_\{x\backslash to\; 0\}(2x+6)=6,$ то есть при $x\backslash to\; 0$ функции $f(x)=2x^2+6x$ и $g(x)=x$ являются бесконечно малыми величинами одного порядка.

В данном случае справедливы записи $2x^2+6x\; =\; O(x)$ и $x\; =\; O(2x^2+6x).$

• При $\{x\backslash to\; 0\}$ бесконечно малая величина $2x^3$ имеет третий порядок малости относительно $x$, поскольку $\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{2x^3\}\{x^3\}=2$, бесконечно малая $0\{,\}7x^2$ - второй порядок, бесконечно малая $\backslash sqrt\{x\}$ - порядок 0,5.

Эквивалентные величины

Определение

Если $\backslash lim\backslash limits\_\{x\backslash to\; a\}\backslash dfrac\{\backslash beta\}\{\backslash alpha\}=1$, то бесконечно малые или бесконечно большие величины $\backslash alpha$ и $\backslash beta$ называются эквивалентными (обозначается как $\backslash alpha\backslash thicksim\backslash beta$).

Очевидно, что эквивалентные величины являются частным случаем бесконечно малых (бесконечно больших) величин одного порядка малости.

При $$ справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):

• $\backslash sin\backslash alpha(x)\backslash thicksim\backslash alpha(x);$
• $\backslash mathrm\{tg\}\backslash ,\backslash alpha(x)\backslash thicksim\backslash alpha(x);$
• $\backslash arcsin\{\backslash alpha(x)\}\backslash thicksim\backslash alpha(x);$
• $\backslash mathrm\{arctg\}\backslash ,\backslash alpha(x)\backslash thicksim\backslash alpha(x);$
• $\backslash log\_a(1+\backslash alpha(x))\backslash thicksim\backslash alpha(x)\backslash cdot\backslash frac\{1\}\{\backslash ln\{a\}\}$, где $a>0$;
• $\backslash ln(1+\backslash alpha\; (x))\backslash thicksim\backslash alpha(x);$
• $a^\{\backslash alpha(x)\}-1\backslash thicksim\backslash alpha(x)\backslash cdot\backslash ln\{a\}$, где $a>0$;
• $e^\{\backslash alpha(x)\}-1\backslash thicksim\backslash alpha(x);$
• $1-\backslash cos\{\backslash alpha(x)\}\backslash thicksim\backslash frac\{\backslash alpha^2(x)\}\{2\};$
• $(1+\backslash alpha(x))^\backslash mu-1\backslash thicksim\backslash mu\backslash cdot\backslash alpha(x),\backslash quad\backslash mu\backslash in\backslash R$, поэтому используют выражение:

$\backslash sqrt[n]\{1+\backslash alpha(x)\}\backslash approx\backslash frac\{\backslash alpha(x)\}\{n\}+1$, где $\backslash alpha(x)\backslash xrightarrow\{\}0$.

Теорема

Предел частного (отношения) двух бесконечно малых или бесконечно больших величин не изменится, если одну из них (или обе) заменить эквивалентной величиной .

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).

Примеры использования

• Найти $\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{\backslash sin\; 2x\}\{x\}.$

Заменяя $\backslash sin\; 2x$ эквивалентной величиной $2x$, получаем $\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{\backslash sin\; 2x\}\{x\}=\backslash lim\backslash limits\_\{x\backslash to\; 0\}\backslash dfrac\{2x\}\{x\}=2.$

• Найти $\backslash lim\backslash limits\_\{x\backslash to\backslash frac\{\backslash pi\}\{2\}\}\backslash dfrac\{\backslash sin(4\backslash cos\; x)\}\{\backslash cos\; x\}.$

Так как $\backslash sin(4\backslash cos\; x)\backslash thicksim\{4\backslash cos\; x\}$ при $x\backslash to\backslash dfrac\{\backslash pi\}\{2\}$ получим $\backslash lim\backslash limits\_\{x\backslash to\; \backslash frac\{\backslash pi\}\{2\}\}\backslash dfrac\{\backslash sin(4\backslash cos\; x)\}\{\backslash cos\; x\}=\backslash lim\backslash limits\_\{x\backslash to\backslash frac\{\backslash pi\}\{2\}\}\backslash dfrac\{4\backslash cos\; x\}\{\backslash cos\; x\}=4.$

• Вычислить $\backslash sqrt\{1\{,\}2\}$.

Используя формулу : $\backslash sqrt\{1\{,\}2\}\backslash approx\; 1+\backslash frac\{0\{,\}2\}\{2\}=1\{,\}1$, тогда как, используя калькулятор (более точные вычисления), получили: $\backslash sqrt\{1\{,\}2\}\backslash approx\; 1\{,\}095$, таким образом ошибка составила 0,005 (менее 1 %), то есть метод полезен, благодаря своей простоте, при грубой оценке арифметических корней близких к единице.

История

Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок »; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков .

Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа , который доказал, что первоначальная точка зрения - актуальные бесконечно малые - также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.

См. также

Напишите отзыв о статье "Бесконечно малая и бесконечно большая"

Примечания

Литература

• // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). - СПб. , 1890-1907.

Отрывок, характеризующий Бесконечно малая и бесконечно большая

– Ну, мой друг, я боюсь, что вы с монахом даром растрачиваете свой порох, – насмешливо, но ласково сказал князь Андрей.
– Аh! mon ami. [А! Друг мой.] Я только молюсь Богу и надеюсь, что Он услышит меня. Andre, – сказала она робко после минуты молчания, – у меня к тебе есть большая просьба.
– Что, мой друг?
– Нет, обещай мне, что ты не откажешь. Это тебе не будет стоить никакого труда, и ничего недостойного тебя в этом не будет. Только ты меня утешишь. Обещай, Андрюша, – сказала она, сунув руку в ридикюль и в нем держа что то, но еще не показывая, как будто то, что она держала, и составляло предмет просьбы и будто прежде получения обещания в исполнении просьбы она не могла вынуть из ридикюля это что то.
Она робко, умоляющим взглядом смотрела на брата.
– Ежели бы это и стоило мне большого труда… – как будто догадываясь, в чем было дело, отвечал князь Андрей.
– Ты, что хочешь, думай! Я знаю, ты такой же, как и mon pere. Что хочешь думай, но для меня это сделай. Сделай, пожалуйста! Его еще отец моего отца, наш дедушка, носил во всех войнах… – Она всё еще не доставала того, что держала, из ридикюля. – Так ты обещаешь мне?
– Конечно, в чем дело?
– Andre, я тебя благословлю образом, и ты обещай мне, что никогда его не будешь снимать. Обещаешь?
– Ежели он не в два пуда и шеи не оттянет… Чтобы тебе сделать удовольствие… – сказал князь Андрей, но в ту же секунду, заметив огорченное выражение, которое приняло лицо сестры при этой шутке, он раскаялся. – Очень рад, право очень рад, мой друг, – прибавил он.
– Против твоей воли Он спасет и помилует тебя и обратит тебя к Себе, потому что в Нем одном и истина и успокоение, – сказала она дрожащим от волнения голосом, с торжественным жестом держа в обеих руках перед братом овальный старинный образок Спасителя с черным ликом в серебряной ризе на серебряной цепочке мелкой работы.
Она перекрестилась, поцеловала образок и подала его Андрею.
– Пожалуйста, Andre, для меня…
Из больших глаз ее светились лучи доброго и робкого света. Глаза эти освещали всё болезненное, худое лицо и делали его прекрасным. Брат хотел взять образок, но она остановила его. Андрей понял, перекрестился и поцеловал образок. Лицо его в одно и то же время было нежно (он был тронут) и насмешливо.
– Merci, mon ami. [Благодарю, мой друг.]
Она поцеловала его в лоб и опять села на диван. Они молчали.
– Так я тебе говорила, Andre, будь добр и великодушен, каким ты всегда был. Не суди строго Lise, – начала она. – Она так мила, так добра, и положение ее очень тяжело теперь.
– Кажется, я ничего не говорил тебе, Маша, чтоб я упрекал в чем нибудь свою жену или был недоволен ею. К чему ты всё это говоришь мне?
Княжна Марья покраснела пятнами и замолчала, как будто она чувствовала себя виноватою.
– Я ничего не говорил тебе, а тебе уж говорили. И мне это грустно.
Красные пятна еще сильнее выступили на лбу, шее и щеках княжны Марьи. Она хотела сказать что то и не могла выговорить. Брат угадал: маленькая княгиня после обеда плакала, говорила, что предчувствует несчастные роды, боится их, и жаловалась на свою судьбу, на свекра и на мужа. После слёз она заснула. Князю Андрею жалко стало сестру.
– Знай одно, Маша, я ни в чем не могу упрекнуть, не упрекал и никогда не упрекну мою жену, и сам ни в чем себя не могу упрекнуть в отношении к ней; и это всегда так будет, в каких бы я ни был обстоятельствах. Но ежели ты хочешь знать правду… хочешь знать, счастлив ли я? Нет. Счастлива ли она? Нет. Отчего это? Не знаю…
Говоря это, он встал, подошел к сестре и, нагнувшись, поцеловал ее в лоб. Прекрасные глаза его светились умным и добрым, непривычным блеском, но он смотрел не на сестру, а в темноту отворенной двери, через ее голову.
– Пойдем к ней, надо проститься. Или иди одна, разбуди ее, а я сейчас приду. Петрушка! – крикнул он камердинеру, – поди сюда, убирай. Это в сиденье, это на правую сторону.
Княжна Марья встала и направилась к двери. Она остановилась.
– Andre, si vous avez. la foi, vous vous seriez adresse a Dieu, pour qu"il vous donne l"amour, que vous ne sentez pas et votre priere aurait ete exaucee. [Если бы ты имел веру, то обратился бы к Богу с молитвою, чтоб Он даровал тебе любовь, которую ты не чувствуешь, и молитва твоя была бы услышана.]
– Да, разве это! – сказал князь Андрей. – Иди, Маша, я сейчас приду.
По дороге к комнате сестры, в галлерее, соединявшей один дом с другим, князь Андрей встретил мило улыбавшуюся m lle Bourienne, уже в третий раз в этот день с восторженною и наивною улыбкой попадавшуюся ему в уединенных переходах.
– Ah! je vous croyais chez vous, [Ах, я думала, вы у себя,] – сказала она, почему то краснея и опуская глаза.
Князь Андрей строго посмотрел на нее. На лице князя Андрея вдруг выразилось озлобление. Он ничего не сказал ей, но посмотрел на ее лоб и волосы, не глядя в глаза, так презрительно, что француженка покраснела и ушла, ничего не сказав.
Когда он подошел к комнате сестры, княгиня уже проснулась, и ее веселый голосок, торопивший одно слово за другим, послышался из отворенной двери. Она говорила, как будто после долгого воздержания ей хотелось вознаградить потерянное время.
– Non, mais figurez vous, la vieille comtesse Zouboff avec de fausses boucles et la bouche pleine de fausses dents, comme si elle voulait defier les annees… [Нет, представьте себе, старая графиня Зубова, с фальшивыми локонами, с фальшивыми зубами, как будто издеваясь над годами…] Xa, xa, xa, Marieie!
Точно ту же фразу о графине Зубовой и тот же смех уже раз пять слышал при посторонних князь Андрей от своей жены.
Он тихо вошел в комнату. Княгиня, толстенькая, румяная, с работой в руках, сидела на кресле и без умолку говорила, перебирая петербургские воспоминания и даже фразы. Князь Андрей подошел, погладил ее по голове и спросил, отдохнула ли она от дороги. Она ответила и продолжала тот же разговор.
Коляска шестериком стояла у подъезда. На дворе была темная осенняя ночь. Кучер не видел дышла коляски. На крыльце суетились люди с фонарями. Огромный дом горел огнями сквозь свои большие окна. В передней толпились дворовые, желавшие проститься с молодым князем; в зале стояли все домашние: Михаил Иванович, m lle Bourienne, княжна Марья и княгиня.
Князь Андрей был позван в кабинет к отцу, который с глазу на глаз хотел проститься с ним. Все ждали их выхода.
Когда князь Андрей вошел в кабинет, старый князь в стариковских очках и в своем белом халате, в котором он никого не принимал, кроме сына, сидел за столом и писал. Он оглянулся.
– Едешь? – И он опять стал писать.
– Пришел проститься.
– Целуй сюда, – он показал щеку, – спасибо, спасибо!
– За что вы меня благодарите?
– За то, что не просрочиваешь, за бабью юбку не держишься. Служба прежде всего. Спасибо, спасибо! – И он продолжал писать, так что брызги летели с трещавшего пера. – Ежели нужно сказать что, говори. Эти два дела могу делать вместе, – прибавил он.
– О жене… Мне и так совестно, что я вам ее на руки оставляю…
– Что врешь? Говори, что нужно.
– Когда жене будет время родить, пошлите в Москву за акушером… Чтоб он тут был.
Старый князь остановился и, как бы не понимая, уставился строгими глазами на сына.
– Я знаю, что никто помочь не может, коли натура не поможет, – говорил князь Андрей, видимо смущенный. – Я согласен, что и из миллиона случаев один бывает несчастный, но это ее и моя фантазия. Ей наговорили, она во сне видела, и она боится.
– Гм… гм… – проговорил про себя старый князь, продолжая дописывать. – Сделаю.
Он расчеркнул подпись, вдруг быстро повернулся к сыну и засмеялся.
– Плохо дело, а?
– Что плохо, батюшка?
– Жена! – коротко и значительно сказал старый князь.
– Я не понимаю, – сказал князь Андрей.
– Да нечего делать, дружок, – сказал князь, – они все такие, не разженишься. Ты не бойся; никому не скажу; а ты сам знаешь.
Он схватил его за руку своею костлявою маленькою кистью, потряс ее, взглянул прямо в лицо сына своими быстрыми глазами, которые, как казалось, насквозь видели человека, и опять засмеялся своим холодным смехом.
Сын вздохнул, признаваясь этим вздохом в том, что отец понял его. Старик, продолжая складывать и печатать письма, с своею привычною быстротой, схватывал и бросал сургуч, печать и бумагу.
– Что делать? Красива! Я всё сделаю. Ты будь покоен, – говорил он отрывисто во время печатания.
Андрей молчал: ему и приятно и неприятно было, что отец понял его. Старик встал и подал письмо сыну.
– Слушай, – сказал он, – о жене не заботься: что возможно сделать, то будет сделано. Теперь слушай: письмо Михайлу Иларионовичу отдай. Я пишу, чтоб он тебя в хорошие места употреблял и долго адъютантом не держал: скверная должность! Скажи ты ему, что я его помню и люблю. Да напиши, как он тебя примет. Коли хорош будет, служи. Николая Андреича Болконского сын из милости служить ни у кого не будет. Ну, теперь поди сюда.
Он говорил такою скороговоркой, что не доканчивал половины слов, но сын привык понимать его. Он подвел сына к бюро, откинул крышку, выдвинул ящик и вынул исписанную его крупным, длинным и сжатым почерком тетрадь.
– Должно быть, мне прежде тебя умереть. Знай, тут мои записки, их государю передать после моей смерти. Теперь здесь – вот ломбардный билет и письмо: это премия тому, кто напишет историю суворовских войн. Переслать в академию. Здесь мои ремарки, после меня читай для себя, найдешь пользу.
Андрей не сказал отцу, что, верно, он проживет еще долго. Он понимал, что этого говорить не нужно.
– Всё исполню, батюшка, – сказал он.
– Ну, теперь прощай! – Он дал поцеловать сыну свою руку и обнял его. – Помни одно, князь Андрей: коли тебя убьют, мне старику больно будет… – Он неожиданно замолчал и вдруг крикливым голосом продолжал: – а коли узнаю, что ты повел себя не как сын Николая Болконского, мне будет… стыдно! – взвизгнул он.
– Этого вы могли бы не говорить мне, батюшка, – улыбаясь, сказал сын.
Старик замолчал.
– Еще я хотел просить вас, – продолжал князь Андрей, – ежели меня убьют и ежели у меня будет сын, не отпускайте его от себя, как я вам вчера говорил, чтоб он вырос у вас… пожалуйста.
– Жене не отдавать? – сказал старик и засмеялся.
Они молча стояли друг против друга. Быстрые глаза старика прямо были устремлены в глаза сына. Что то дрогнуло в нижней части лица старого князя.
– Простились… ступай! – вдруг сказал он. – Ступай! – закричал он сердитым и громким голосом, отворяя дверь кабинета.
– Что такое, что? – спрашивали княгиня и княжна, увидев князя Андрея и на минуту высунувшуюся фигуру кричавшего сердитым голосом старика в белом халате, без парика и в стариковских очках.
Князь Андрей вздохнул и ничего не ответил.
– Ну, – сказал он, обратившись к жене.
И это «ну» звучало холодною насмешкой, как будто он говорил: «теперь проделывайте вы ваши штуки».
– Andre, deja! [Андрей, уже!] – сказала маленькая княгиня, бледнея и со страхом глядя на мужа.
Он обнял ее. Она вскрикнула и без чувств упала на его плечо.
Он осторожно отвел плечо, на котором она лежала, заглянул в ее лицо и бережно посадил ее на кресло.
– Adieu, Marieie, [Прощай, Маша,] – сказал он тихо сестре, поцеловался с нею рука в руку и скорыми шагами вышел из комнаты.
Княгиня лежала в кресле, m lle Бурьен терла ей виски. Княжна Марья, поддерживая невестку, с заплаканными прекрасными глазами, всё еще смотрела в дверь, в которую вышел князь Андрей, и крестила его. Из кабинета слышны были, как выстрелы, часто повторяемые сердитые звуки стариковского сморкания. Только что князь Андрей вышел, дверь кабинета быстро отворилась и выглянула строгая фигура старика в белом халате.
– Уехал? Ну и хорошо! – сказал он, сердито посмотрев на бесчувственную маленькую княгиню, укоризненно покачал головою и захлопнул дверь.

В октябре 1805 года русские войска занимали села и города эрцгерцогства Австрийского, и еще новые полки приходили из России и, отягощая постоем жителей, располагались у крепости Браунау. В Браунау была главная квартира главнокомандующего Кутузова.
11 го октября 1805 года один из только что пришедших к Браунау пехотных полков, ожидая смотра главнокомандующего, стоял в полумиле от города. Несмотря на нерусскую местность и обстановку (фруктовые сады, каменные ограды, черепичные крыши, горы, видневшиеся вдали), на нерусский народ, c любопытством смотревший на солдат, полк имел точно такой же вид, какой имел всякий русский полк, готовившийся к смотру где нибудь в середине России.

Функция называется бесконечно малой при
или при
, если
или
.

Например: функция
бесконечно малая при
; функция
бесконечно малая при
.

Замечание 1. Никакую функцию без указания направления изменения аргумента бесконечно малой назвать нельзя. Так, функция
при
является бесконечно малой, а при
она уже не является бесконечно малой (
).

Замечание 2. Из определения предела функции в точке, для бесконечно малых функций выполняется неравенство
.Этим фактом мы в дальнейшем будем неоднократно пользоваться.

Установим некоторые важные свойства бесконечно малых функций.

Теорема (о связи функции, её предела и бесконечно малой): Если функция
может быть представлена в виде суммы постоянного числаА и бесконечно малой функции
при
, то число

Доказательство:

Из условия теоремы следует, что функция
.

Выразим отсюда
:
. Поскольку функция
бесконечно малая, для неё справедливо неравенство
, тогда для выражения (
) также выполняется неравенство

А это значит, что
.

Теорема (обратная): если
, то функция
может быть представлена в виде суммы числаА и бесконечно малой при
функции
, т.е.
.

Доказательство:

Так как
, то для
выполняется неравенство
(*) Рассмотрим функцию
как единую и неравенство (*) перепишем в виде

Из последнего неравенства следует, что величина (
) является бесконечно малой при
. Обозначим её
.

Откуда
. Теорема доказана.

Теорема 1 . Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Доказательство:

Проведём доказательство для двух слагаемых, так как для любого конечного числа слагаемых оно приводится аналогично.

Пусть
и
бесконечно малые при
функции и
– сумма этих функций. Докажем, что для
, существует такое
, что для всехх , удовлетворяющих неравенству
, выполняется неравенство
.

Так как функция
бесконечно малая функция,
, что для всех
выполняется неравенство
.

Так как функция
бесконечно малая функция,
, а следовательно существует такое, что для всех
выполняется неравенство
.

Возьмём равным меньшему из чисели, тогда в–окрестности точкиа будут выполняться неравенства
,
.

Составим модуль функции
и оценим его значение.

То есть
, тогда функция бесконечно малая, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции
при
на ограниченную функцию
есть бесконечно малая функция.

Доказательство:

Так как функция
ограниченная, то существует такое положительное число
, что для всехвыполняется неравенство
.

Так как функция
бесконечно малая при
, то существует такая–окрестность точки, что для всехих этой окрестности выполняется неравенство
.

Рассмотрим функцию
и оценим её модуль

Итак
, а тогда
– бесконечно малая.

Теорема доказана.

Теоремы о пределах.

Теорема 1. Предел алгебраической суммы конечного числа функций равен алгебраической сумме пределов этих функций

Доказательство:

Для доказательства достаточно рассмотреть две функции, это не нарушит общности рассуждений.

Пусть
,
.

По теореме о связи функции, её предела и бесконечно малой, функции
и
можно представить в виде
где
и
– бесконечно малые при
.

Найдём сумму функций
и

Величина
есть постоянная величина,
– величина бесконечно малая. Таким образом, функция
представлена в виде суммы постоянной величины и бесконечно малой функции.

Тогда число
является пределом функции
, т.е.

Теорема доказана.

Теорема 2 . Предел произведения конечного числа функций равен произведению пределов этих функций

Доказательство:

Не нарушая общности рассуждений, проведём доказательство для двух функций
и
.

Пусть , тогда
,

Найдём произведение функций
и

Величина
есть постоянная величина,бесконечно малая функция. Следовательно, число
является пределом функции
, то есть справедливо равенство

Следствие:
.

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля

.

Доказательство: Пусть
,

Тогда
,
.

Найдём частное и проделаем над ним некоторые тождественные преобразования

Величина постоянная, дробь
бесконечно малая. Следовательно, функцияпредставлена в виде суммы постоянного числа и бесконечно малой функции.

Тогда
.

Замечание. Теоремы 1–3 доказаны для случая
. Однако, они могут быть применимы при
, поскольку доказательство теорем в этом случае проводится аналогично.

Например. Найти пределы:

Первый и второй замечательные пределы.

Функция не определена при
. Однако её значения в окрестности точки нуль существуют. Поэтому можно рассматривать предел этой функции при
. Этот предел носит названиепервого замечательного предела .

Он имеет вид:
.

Например . Найти пределы: 1.
. Обозначают
, если
, то
.
; 2.
. Преобразуем данное выражение так, чтобы предел свёлся к первому замечательному пределу.
; 3..

Рассмотрим переменную величину вида
, в которойпринимает значения натуральных чисел в порядке их возрастания. Дадимразличные значения: если

Давая следующие значения из множества
, нетрудно увидеть, что выражение
при
будет
. Более того, доказывается, что
имеет предел. Этот предел обозначается буквой:
.

Число иррациональное:
.

Теперь рассмотрим предел функции
при
. Этот предел называетсявторым замечательным пределом

Он имеет вид
.

Например.

а)
. Выражение
заменим произведениемодинаковых сомножителей
, применим теорему о пределе произведения и второй замечательный предел; б)
. Положим
, тогда
,
.

Второй замечательный предел используется взадаче о непрерывном начислении процентов

При начислении денежных доходов по вкладам часто пользуются формулой сложных процентов, которая имеет вид:

,

где - первоначальный вклад,

- ежегодный банковский процент,

- число начислений процентов в год,

- время, в годах.

Однако, в теоретических исследованиях при обосновании инвестиционных решений чаще пользуются формулой экспоненциального (показательного) закона роста

.

Формула показательного закона роста получена как результат применения второго замечательного предела к формуле сложных процентов

Непрерывность функций.

Рассмотрим функцию
определённую в некоторой точкеи некоторой окрестности точки. Пусть в указанной точке функция имеет значение
.

Определение 1. Функция
называется непрерывной в точке , если она определена в окрестности точки, включая саму точку и
.

Определение непрерывности можно сформулировать иначе.

Пусть функция
определена при некотором значении,
. Если аргументудать приращение
, то функция получит приращение

Пусть функция в точке непрерывна (по первому определению непрерывности функции в точке),

То есть, если функция непрерывна в точке , то бесконечно малому приращению аргумента
в этой точке соответствует бесконечно малое приращение функции.

Справедливо и обратное предложение: если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна.

Определение 2. Функция
называется непрерывной при
(в точке), если она определена в этой точке и некоторой её окрестности и если
.

Учитывая первое и второе определение непрерывности функции в точке можно получить следующее утверждение:

или
, но
, тогда
.

Следовательно, для того чтобы найти предел непрерывной функции при
достаточно в аналитическое выражение функции вместо аргументаподставить его значение.

Определение 3. Функция, непрерывная в каждой точке некоторой области называется непрерывной в этой области.

Например:

Пример 1. Доказать, что функция
непрерывна во всех точках области определения.

Воспользуемся вторым определением непрерывности функции в точке. Для этого возьмём любое значение аргумента и дадим ему приращение
. Найдём соответствующее приращение функции

Пример 2. Доказать, что функция
непрерывна во всех точкахиз
.

Дадим аргументу приращение
, тогда функция получит приращение

Найдём так как функция
, то есть ограничена.

Аналогично можно доказать, что все основные элементарные функции непрерывны во всех точках области их определения, то есть область определения элементарной функции совпадает с областью её непрерывности.

Определение 4. Если функция
непрерывна в каждой точке некоторого интервала
, то говорят, что функция непрерывна на этом интервале.

Приводится определение бесконечно малой последовательности. Она обладает свойствами сходящихся последовательностей. Также имеются свойства, характерные только для последовательностей с пределом равным нулю. Приводятся доказательства таких свойств. Рассмотрен пример, в котором нужно доказать, что последовательность бесконечно малая.

Содержание

Определение

Бесконечно малая последовательность { α n } - это сходящаяся последовательность, предел которой равен нулю:
.

Следующие свойства являются прямым следствием арифметических свойств , примененных к последовательностям, предел которых равен нулю.

Свойство суммы и разности бесконечно малых последовательностей

Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Также линейная комбинация конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Доказательство предела суммы и разности числовых последовательностей .

Свойство произведения бесконечно малых последовательностей

Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Доказательство предела произведения числовых последовательностей .

Следующие свойства относятся только к бесконечно малым последовательностям и не являются прямым следствием свойств сходящихся последовательностей.

{ x n }
x n = b + α n ,
где { α n }

Доказательства свойств

Свойство произведения ограниченной последовательности на бесконечно малую

Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Доказательство

Пусть последовательность ограничена некоторым числом :
(3.1) .

Пусть последовательность - бесконечно малая. То есть имеется такая функция , зависящая от переменной , что для любого положительного значения переменной , выполняется неравенство
(3.2) при .

Пусть последовательность является произведением последовательностей и . Ее общий член имеет вид:
.
Нам нужно найти такую функцию , при которой выполняется неравенство
(3.3) при .

Применим (3.1) и (3.2):
.
Это выполняется при . Итак,
.
Положим :
.

То есть мы нашли такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(3.3) при .

Свойство доказано.

Свойство представления сходящейся последовательности через бесконечно малую

Для того, чтобы последовательность { x n } имела предел b , необходимо и достаточно, чтобы
x n = b + α n ,
где { α n } - бесконечно малая последовательность.

Доказательство

Необходимость . Пусть . Рассмотрим последовательность с общим членом . Используем арифметические свойства пределов :
.
То есть - бесконечно малая последовательность.

Достаточность . Пусть . На основании арифметических свойств пределов имеем:
.

Свойство доказано.

Пример

Все примеры Используя определение предела последовательности доказать, что последовательность

является бесконечно малой.

Выпишем определение бесконечно малой последовательности:
.
Поскольку n является натуральным числом, n = 1, 2, 3, ... , то
,
,
.
Поэтому члены последовательности являются положительными числами. Тогда
.

Итак, мы получили следующую оценку:
.
Вводим положительные числа и :
.
Согласно свойствам неравенств , если и , то
.

Отсюда следует, что для любого положительного можно найти натуральное число , так что при ,
.
Это означает, что предел исходной последовательности равен нулю и, следовательно, она является бесконечно малой.

Сравнение бесконечно малых функций, эквивалентные функции

Бесконечно малые и бесконечно большие величины.

О.1. Последовательность называется бесконечно большой, если для любого положительного числа А (сколь большим бы мы его не взяли) существует номер N такой, что при n›N выполняется неравенство | х п | › А, т.е. какое бы большое число А мы не взяли, найдется такой номер, начиная с которого все члены последовательности окажутся больше А.

Определение 6 . Последовательность {α п } называется бесконечно малой, если для любого положительного числа ε (сколь малым бы мы его не взяли) существует номер N такой, что при n›N выполняется неравенство | α п | ‹ε.

1. Последовательность {п} является бесконечно большой.

2. Последовательность {} является бесконечно малой.

Теорема 1. Если {х п } - бесконечно большая последовательность и все ее члены отличны от нуля, х п ≠0, то последовательность {α п }=- бесконечно малая, и, обратно, если {α п } бесконечно малая последовательность, α п ≠0, то последовательность {х п }=бесконечно большая.

Сформулируем основные свойства бесконечно малых последовательностей в виде теорем.

Теорема 2. Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности.

Пример 2. Последовательность с общим членом бесконечно малая, т.к. т.е заданная последовательность является суммой бесконечно малых последовательностей и и поэтому является бесконечно малой.

Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 3. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Замечание. Частное двух бесконечно малых последовательностей может быть любой последовательностью и может не иметь смысла.

Например, если , , то все элементы последовательности равны 1 и данная последовательность является ограниченной. Если , , то последовательность - бесконечно большая, и наоборот, если , а , то - бесконечно малая последовательность. Если начиная с некоторого номера элементы последовательности равны нулю, то последовательность не имеет смысла.

Теорема 4. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.

Пример 3. Последовательность бесконечно малая, т.к. и последовательность {}- бесконечно малая, последовательность - ограничена, т.к. ‹ 1. Следовательно, - бесконечно малая последовательность.

Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Определение. Функция f(x) называется бесконечно большой при , если для любого, даже сколь угодно большого положительного числа , найдется такое положительное число (зависящее от М, δ=δ(М)), что для всех х, не равных х 0 и удовлетворяющих условию , выполняется неравенство

Записывают: или при .

Например, функция есть бесконечно большая функция при ; функция при .

Если f(x) стремится к бесконечности при и принимает лишь положительные значения, то пишут , если лишь отрицательные значения, то .

Определение. Функция f(x), заданная на всей числовой прямой, называется бесконечно большой при , если для любого положительного числа , найдется такое положительное число (зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию , выполняется неравенство

Например, функция у=2 х есть бесконечно большая функция при ; функция является бесконечно большой функцией при .

Свойства бесконечно больших функций:

1. Произведение б.б.ф. на функцию, предел которой отличен от нуля, есть б.б.ф.

2. Сумма б.б.ф. и ограниченной функции есть б.б.ф.

3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф.

Например, если функция f(x)=tgx есть б.б.ф. при , функция φ(х)=4х-3 при имеет предел (2π-3) отличный от нуля, а функция ψ(х)=sinx – ограниченная функция, то

f(x) φ(х)=(4х-3) tgx; f(x) + ψ(х)= tgx + sinx; есть бесконечно большие функции при .

Определение. Функция f(x) называется бесконечно малой при , если

По определению предела функции равенство (1) означает: для любого, даже сколь угодно малого положительного числа , найдется такое положительное число (зависящее от ε, δ=δ(ε)), что для всех х, не равных х 0 и удовлетворяющих условию , выполняется неравенство

Теорема. Для выполнения равенства необходимо и достаточно, чтобы функция была бесконечно малой при . При этом функция может быть представлена в виде .

Аналогично определяется б.м.ф. при ,- 0, , во всех случаях f(x)0.

Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, β и т.д.

Например, у=х 2 при х→0; у=х-2 при х→2; у=sinx при х→πк, - бесконечно малые функции.

Свойства бесконечно малых функций:

1. Сумма конечного числа бесконечно малых функций есть величина бесконечно малая;

2. Произведение конечного числа бесконечно малых функций, а также бесконечно малой функции на ограниченную функция, есть величина бесконечно малая;

3. Частное от деления бесконечно малой функции на функцию, предел которой не равен нолю, если величина бесконечно малая.

Рассмотрим последнее свойство при если функции и являются бесконечно малыми (Сравнение бесконечно малых функций):

1). Если , то называется бесконечно малой, более высокого порядка малости, чем .

Пример . При х→2 функция (х - 2) 3 бесконечно малая более высокого порядка, чем (х -2), так как .

2). Если , то и называются бесконечно малыми одного порядка (имеют одинаковую скорость стремления к нолю);

Пример . При х→0 функции 5х 2 и х 2 являются бесконечно малыми одного порядка, так как .

3). Если ,то и называются эквивалентными бесконечно малыми, обозначаются ~., то

Связь между бесконечно малыми и бесконечно большими функциями: функция обратная бесконечно малой является бесконечно большой (и наоборот), т.е. если - бесконечно малая функция, то - бесконечно большая.

БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА

Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x) , где a(x) – бесконечно малая при x→a.

Доказательство .

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство . Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x) , где и . Нам нужно доказать, что при произвольном как угодно малом ε> 0 найдется δ> 0, такое, что для x , удовлетворяющих неравенству |x – a|<δ , выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε> 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ 1 > 0, что при |x – a|< δ 1 имеем |α(x)|< ε/ 2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ 2 > 0, что при |x – a|< δ 2 имеем | β(x)|< ε/ 2.

Возьмем δ=min{ δ 1 , δ 2 } .Тогда в окрестности точки a радиуса δ будет выполняться каждое из неравенств |α(x)|< ε/ 2 и | β(x)|< ε/ 2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x) | ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|< ε, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞ ) есть бесконечно малая функция.

Доказательство . Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a , то для произвольного ε> 0 найдется окрестность точки a , в которой будет выполняться неравенство |α(x)|< ε/M . Тогда в меньшей из этих окрестностей имеем | αf|< ε/M = ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

Из доказанной теоремы вытекают:

Следствие 1. Если и , то .

Следствие 2. Если и c= const, то .

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x) , предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство . Пусть . Тогда 1/f(x) есть ограниченная функция. Поэтому дробь есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ

Теорема 1. Если функция f(x) является бесконечно большой при x→a , то функция 1/f(x) является бесконечно малой при x→a .

Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x , для которых |x – a|<δ , выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a , то найдется δ>0 такое, что как только |x – a|<δ , так |f(x)|> 1/ ε. Но тогда для тех же x .

Примеры.

Можно доказать и обратную теорему.

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y= 1/f(x) является бесконечно большой функцией.

Доказательство теоремы проведите самостоятельно.

Примеры.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A ≠ 0

ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

Доказательство . Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и g(x)=c+β(x) , где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)) .

Так как b + c есть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

Пример. .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

Доказательство . Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Пример. .

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

Доказательство . Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) , где α, β – бесконечно малые. Рассмотрим частное

Дробь является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c 2 ≠0.

Примеры.

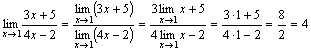
Теорема 4. Пусть даны три функции f(x), u(x) и v(x) , удовлетворяющие неравенствам u(x)≤f(x)≤ v(x) . Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞ ), то и функция f(x) стремится к тому же пределу, т.е. если

, то .

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞ ) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b , то этот предел не может быть отрицательным: b≥0 .

Доказательство . Доказательство проведем методом от противного. Предположим, что b<0 , тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a . Но тогда y не стремится к пределу b при x→a , что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы , то имеет место неравенство b≥c .

Доказательство. По условию теоремы f(x)-g(x) ≥0 , следовательно, по теореме 5 , или .

ОДНОСТОРОННИЕ ПРЕДЕЛЫ

До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a , слева или справа от a . Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a , оставаясь с одной стороны от а , слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что x принимает только значения, меньшие a , то пишут и называют bпределом функции f(x) в точке a слева.