1. Учить детей соблюдать основы безопасности.
2. Формировать представления о том, что играть с огнём опасно, в отсутствии взрослых нельзя пользоваться электроприборами, без разрешения взрослых не трогать колющие, режущие, острые предметы и медикаменты.
3. Учить правильно вести себя с незнакомыми людьми.
4. В случаи необходимости самостоятельно набирать телефоны пожарной службы, полиции и скорой помощи.
5. Формировать чувство ответственности за свои поступки и личное отношение к соблюдению и нарушению правил безопасного поведения.
6. Развивать внимание, логическое мышление, память.

Предварительная работа:

1. Проведение занятий по обучению дошкольников основам безопасности.
2. Чтение художественной литературы по ОБЖ.
3. Загадывание и отгадывание загадок по ОБЖ.

Ход развлечения:

Под веселую музыку дети заходят в зал, который оформлен под детскую комнату, и садятся на стульчики.

Вдруг, появляется… Малыш (персонаж из сказки А. Линдгрен «Малыш и Карлсон»). Он прикрывает глаза руками и движется в сторону сидящих детей.

Малыш: Ку-Ку!... Ку-ку!... Ку-ку!... (приближается к детям)

Ой! А вы кто такие?

Дети отвечают.

Малыш: А я – Малыш. Меня так зовут, и я здесь живу. Это мой дом и моя комната. Я играл в «Прятки» с моим другом Карлсоном. Вы его не видел?..

А давайте я с вами тоже буду дружить! Ведь это так здорово, когда у тебя много друзей, и все они приходят в гости! Хотите со мной дружить?...

А что вы делаете, когда дружите?.. Играете?! А давайте я с вами в «Прятки» поиграю. Только в музыкальные!

Музыкальная игра «Я от тебя убегу-убегу…»

Малыш: Ну всё-таки, где же Карлсон? .. А давайте его позовём!

Все зовут Карлсона, и он появляется с пустой банкой из-под варенья в руках

Карлсон: Привет, друзья! Привет… А вы что делаете?

Дети: Играем!

Карлсон: А давайте лучше шалить! Это веселее!

Дети и Малыш: Мы не умеем!

Карлсон: Я научу! Я как раз с собой прихватила очень полезные вещи – кнопки, иголки, гвозди… Давайте их взрослым на стулья подложим! Вот смеха будет, если они на них сядут…

Малыш: Карлсон, а ты уверен, что это будет весело?.. А если иголка тебе вопьётся в палец?...

Карлсон: Вот об этом я не подумал… Хорошо, что ты меня, Малыш, предупредил. Я ведь мог серьёзно пораниться! Ладно, не будем шалить с кнопками. А что же…? При думал! Давайте тогда ФЕЙЕРВЕРК устроим! Вы знаете, что такое фейерверк?..

У меня в кармане большущий гвоздь завалялся. Вот он! Надо его в розетку засунуть! Вот треску будет! Пс-пс-пс…! Как будто много-много шариков лопается! Настоящий фейерверк получится!

Малыш: Карлсон, опять ты за своё! Это же очень опасно!

Карлсон: Почему опасно?

Дети объясняют Карлсону, почему нельзя ничего засовывать в розетку.

Малыш: Карлсон, давай лучше вместе с ребятами поиграем в игру «Шарики и иголочка» Это будет весело! А главное – БЕЗОПАСНО!!!

Игра «Шарики и иголочка»

Карлсон и Малыш – «иголочки», а дети – «шарики». Под музыку дети- «шарики» бегают по залу, а Карлсон и Малыш их догоняют и «лопают»

Карлсон: Всё! Хватит бегать! От вашего шума у меня голова разболелась! Я теперь самый больной и несчастный на свете! Ох! Нужно мне срочно оказать помощь.

Малыш! Я тут у тебя Аптечку видел с лекарствами… Вот она. Что бы мне выпить от головной боли?…

А! Съем все таблетки. Какая-нибудь из них мне поможет.

Карлсон хочет выпить таблетки, но Малыш выбивает у него из рук флакончики. Таблетки-пилюли (разноцветные) рассыпаются.

Карлсон: Ты что наделал?

Малыш: нельзя глотать лекарства просто так!

Карлсон: Почему?

Дети объясняют, почему опасно принимать просто так лекарства.

Карлсон: Ой, от страха у меня даже головная боль прошла! Я всё понял! С лекарствами надо обращаться очень осторожно, и принимать их только тогда, когда велит доктор! А что же нам с этими пилюлями теперь делать?...

Малыш: А давай их быстро соберем, а ребят попросим нам помочь. Можно даже посоревноваться – кто быстрее соберет пилюли! Красненькие будем собирать вот в эту бутылочку, белые в эту, а желтые – вот в эту. А помогут нам это сделать Ваня, Егор и Таня…

Игра «Кто быстрее соберёт»

Малыш: Ой, я совсем забыл! Мама просила меня в магазин сходить за хлебом! Я быстро! Одна нога тут, другая –там…

(Малыш уходит переодеваться в костюм Жулика.)

Карлсон: Что-то меня знобить стало… Я, наверное, точно заболел. У вас спички есть?.. Сейчас костер разведем, погреемся.

Комментарии детей.

Карлсон: Ребята, а давайте тогда понарошку будем тушить пожар.

Аттракцион «Осторожно огонь!»

Карлсон делит детей на 2 команды и предлагает детям «потушить» огонь синей водичкой (маркером). Каждая команда закрашивает синим маркером огонь на нарисованном домике, чтобы спасти его от пожара.

Карлсон: А я знаю что делать, если случится пожар. А вы знаете?

Ответы детей

Карлсон: Ну а теперь давайте наконец начнём шалить!... А, может, на люстре покатаемся?.. А родители нас подсадят и раскачают!

Комментарии детей.

Тогда давайте откроем окна, сядем на подоконник и будем болтать ногами.

Комментарии детей.

Раздается «звонок в дверь»!

Карлсон: Ещё гости пожаловали?! Надо открыть!.. или не открывать?.. Вдруг это Жулик? И он хочет нас обидеть?.. А ещё говорят, что сейчас по квартирам ходит Баба Яга и крадёт детей… Испугались? Да я пошутил!

Раздается повторный «звонок в дверь»!

А!!! Открою! Даже если там и Жулик… Жулик-то один, а нас много! Мы ведь ничего с вами не боимся! Правда?... Но, на всякий случай, я открою и быстро спрячусь… (прячется).

Звучит таинственная музыка. Появляется Жулик в плаще и маске.

Жулик: Ага! Кажется, хозяев нет дома. Одни дети и много ценностей. Детки, сидите тихо, тогда я не сделаю вам ничего плохого. О! Телевизор, пылесос, чайник, микроволновка… (начинает все собирать в сумку) Хороший у меня улов сегодня!

Вдруг, под музыку влетает приведение в простыне (это Карлсон). «Приведение – Карлсон» гоняется за Жуликом. Жулик бросает сумку с вещами. Всё рассыпается … Жулик убегает. Карлсон снимает с себя белое покрывало «Приведения»…

Карлсон: Здорово я его напугал! Хорошо, что всё так закончилось! Может нельзя дверь открывать незнакомцам? Ребята, как вы думаете? Или вы тоже всем подряд дверь открываете?..

Карлсон беседует с детьми. Возвращается Малыш из магазина.

Малыш: Вот я и вернулся! (Видит разбросанные вещи.) А что у вас тут случилось?

Дети рассказывают о том, что произошло.

Малыш: Карлсон, разве ты не знал, что нельзя открывать дверь незнакомым людям. Надо сначала посмотреть в дверной глазок или спросить: «Кто?»

И если за дверью незнакомый тебе человек, дверь ни в коем случае не открывать!

Карлсон: А если незнакомец скажет, что он из полиции ...?

Малыш: Ребята, как вы думаете, нужно ли открыть дверь в этом случае?...

Ответы детей

Ребенок читает стихотворение:

Не пускайте дядю в дом, если дядя незнаком!

И не открывайте тете, если мама на работе,

Ведь преступник, он – хитер, притворится, что монтер.

Или даже скажет он, что пришел к вам почтальон.

Чтоб тебя не обокрали, не схватили, не украли,

Незнакомцам ты не верь, закрывай покрепче дверь!

Малыш: Карлсон, надеюсь, ты понял, что и дома нас подстерегают разные опасности. И надо всегда помнить о правилах безопасного поведения дома. Особенно если ты остался дома один!

Карлсон, я хочу проверить, как ты всё понял!

Карлсон: А чего всё я, да я?... Давай и ребят проверяй тоже. Вдруг они чего-нибудь не поняли…

Малыш проводит игру «Запрещается – разрешается»

Детям и Карлсону предлагается правильно разложить картинки, на которых изображены разные предметы (опасные и не опасные) и различные ситуации (опасные и не опасные), в две коробочки (красную «Запрещающую» и зелёную «Разрешающую»).

После игры Малыш и Карлсон прощаются с детьми и желают им оставаться такими же умными, благоразумными и осмотрительными!

Если вы поклонник фильмов про Мстителей, первое, что может прийти вам на ум, когда вы услышите слово «Tesseract», это прозрачный кубообразный сосуд Камня бесконечности, содержащий безграничную силу.

Для поклонников Вселенной Marvel Тессеракт — это светящийся синий куб, от которого люди с не только Земли, но и других планет тоже сходят с ума. Вот почему все Мстители объединились, чтобы защитить Землян от чрезвычайно разрушительных сил Тессеракта.

Однако нужно сказать следующее: Тессеракт — это фактическое геометрическое понятие, а точнее, форма, существующая в 4D. Это не просто синий куб от Мстителей … это реальная концепция.

Тессеракт — это объект в 4 измерениях. Но прежде чем мы подробно объясним его, давайте начнем с самого начала.

Что такое «измерение»?

Каждый человек слышал термины 2D и 3D, представляя соответственно двумерные или трехмерные объекты пространства. Но что представляют собой эти измерения?

Измерение — это просто направление, в котором вы можете пойти. Например, если вы рисуете линию на листе бумаги, вы можете идти либо влево / вправо (по оси x), либо в направлении вверх / вниз (ось y). Таким образом, мы говорим, что бумага двумерна, так как вы можете идти только в двух направлениях.

В 3D есть ощущение глубины.

Теперь, в реальном мире, помимо упомянутых выше двух направлений (слева / справа и вверх / вниз), вы также можете пойти «в / из». Следовательно, в 3D-пространстве добавляется ощущение глубины. Поэтому мы говорим, что реальная жизнь 3-мерная.

Точка может представлять 0 измерений (поскольку она не перемещается в любом направлении), линия представляет 1 измерение (длина), квадрат представляет 2 измерения (длина и ширина), а куб представляет 3 измерения (длина, ширина и высота).

Возьмите 3D-куб и замените каждую его грань (которая в настоящее время является квадратом) кубом. И вот! Форма, которую вы получаете, — это и есть тессеракт.

Что такое тессеракт?

Проще говоря, тессеракт — это куб в 4-мерном пространстве. Вы также можете сказать, что это 4D-аналог куба. Это 4D-форма, где каждая грань является кубом.

3D-проекция тессеракта, выполняющая двойное вращение вокруг двух ортогональных плоскостей.
Изображение: Jason Hise

Вот простой способ концептуализации размеров: квадрат — двумерный; поэтому каждый из его углов имеет 2 линии, отходящих от него под углом 90 градусов друг к другу. Куб — 3D, поэтому каждый из его углов имеет 3 линии, сходящие с него. Аналогичным образом, тессеракт представляет собой 4D-форму, поэтому каждый угол имеет 4 линии, отходящих от него.

Почему трудно представить себе тессеракт?

Поскольку мы, как люди, эволюционировали, чтобы визуализировать объекты в трех измерениях, все, что входит в дополнительные измерения, такие как 4D, 5D, 6D и т. д., не имеет для нас большого смысла, потому что мы вообще не можем их представить. Наш мозг не может понять 4-го измерения в пространстве. Мы просто не можем об этом думать.

Однако только потому, что мы не можем визуализировать концепцию многомерных пространств, это не значит, что она не может существовать.

В геометрии гиперкуб - это n -мерная аналогия квадрата (n = 2) и куба (n = 3). Это замкнутая выпуклая фигура, состоящая из групп параллельных линий, расположенных на противоположных краях фигуры, и соединенных друг с другом под прямым углом.

Эта фигура также известная под названием тессеракт (tesseract). Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.

Согласно Окфордскому словарю английского языка, слово "tesseract" было придумано в 1888 Чарльзом Говардом Хинтоном (Charles Howard Hinton) и использовано в его книге "Новая эра мысли" ("A New Era of Thought"). Слово было образовано от греческого "τεσσερες ακτινες" ("четыре луча"), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).

n -мерный гиперкуб также называется n-кубом .

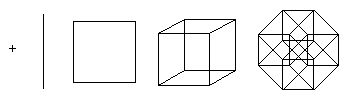
Точка - это гиперкуб размерности 0. Если сдвинуть точку на единицу длины, получится отрезок единичной длины - гиперкуб размерности 1. Далее, если сдвинуть отрезок на единицу длины в направлении перпендикулярном направлению отрезка получится куб - гиперкуб размерности 2. Сдвигая квадрат на единицу длины в направлении перпендикулярном плоскости квадрата, получается куб - гиперкуб размерности 3. Этот процесс может быть обобщен на любое количество измерений. Например, если сдвинуть куб на единицу длины в четвертом измерении, получится тессеракт.

Семейство гиперкубов является одним из немногих правильных многогранников, которые могут быть представлены в любом измерении.

Элементы гиперкуба

Гиперкуб размерности n имеет 2n "сторон" (одномерная линия имеет 2 точки; двухмерный квадрат - 4 стороны; трехмерный куб - 6 граней; четырехмерный тессеракт - 8 ячеек). Количество вершин (точек) гиперкуба равно 2 n (например, для куба - 2 3 вершин).

Количество m -мерных гиперкубов на границе n -куба равно

Например, на границе гиперкуба находятся 8 кубов, 24 квадрата, 32 ребра и 16 вершин.

Элементы гиперкубов

n-куб	Название	Вершина (0-грань)	Ребро (1-грань)	Грань (2-грань)	Ячейка (3-грань)	(4-грань)	(5-грань)	(6-грань)	(7-грань)	(8-грань)
0-куб	Точка	1
1-куб	Отрезок	2	1
2-куб	Квадрат	4	4	1
3-куб	Куб	8	12	6	1
4-куб	Тессеракт	16	32	24	8	1
5-куб	Пентеракт	32	80	80	40	10	1
6-куб	Хексеракт	64	192	240	160	60	12	1
7-куб	Хептеракт	128	448	672	560	280	84	14	1
8-куб	Октеракт	256	1024	1792	1792	1120	448	112	16	1
9-куб	Эненеракт	512	2304	4608	5376	4032	2016	672	144	18

Проекция на плоскость

Формирование гиперкуба может быть представлено следующим способом:

• Две точки A и B могут быть соединены, образуя отрезок AB.
• Два параллельных отрезка AB и CD могут быть соединены, образуя квадрат ABCD.
• Два параллельных квадрата ABCD и EFGH могут быть соединены, образуя куб ABCDEFGH.
• Два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены, образуя гиперкуб ABCDEFGHIJKLMNOP.

Последнюю структуру нелегко представить, но возможно изобразить ее проекцию на двухмерное или трехмерное пространство. Более того, проекции на двухмерную плоскость могут быть более полезны возможностью перестановки позиций спроецированных вершин. В этом случае можно получить изображения, которые больше не отражают пространственные отношения элементов внутри тессеракта, но иллюстрируют структуру соединений вершин, как на примерах ниже.

На первой иллюстрации показано, как в принципе образуется тессеракт путем соединения двух кубов. Эта схема похожа на схему создания куба из двух квадратов. На второй схеме показано, что все ребра тессеракта имеют одинаковую длину. Эта схема также заставляют искать соединенные друг с другом кубы. На третьей схеме вершины тессеракта расположены в соответствии с расстояниями вдоль граней относительно нижней точки. Эта схема интересна тем, что она используется как базовая схема для сетевой топологии соединения процессоров при организации параллельных вычислений: расстояние между любыми двумя узлами не превышает 4 длин ребер, и существует много различных путей для уравновешивания нагрузки.

Гиперкуб в искусстве

Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт Хайнлайн в рассказе "Дом, который построил Тил" ("And He Built a Crooked House") описал дом, построенный по форме развертки тессеракта. В рассказе этот Далее этот дом сворачивается, превращаясь в четырехмерный тессеракт. После этого гиперкуб появляется во многих книгах и новеллах.

В фильме "Куб 2: Гиперкуб" рассказывается о восьми людях, запертых в сети гиперкубов.

На картине Сальвадора Дали "Распятие" ("Crucifixion (Corpus Hypercubus)", 1954) изображен Иисус распятый на развертке тессеракта. Эту картину можно увидеть в Музее Искусств (Metropolitan Museum of Art) в Нью-Йорке.

Заключение

Гиперкуб - одна из простейших четырехмерных объектов, на примере которого можно увидеть всю сложность и необычность четвертого измерения. И то, что выглядит невозможным в трех измерениях, возможно в четырех, например, невозможные фигур. Так, например, бруски невозможного треугольника в четырех измерениях будут соединены под прямыми углами. И эта фигура будет выглядеть так со всех точек обзора, и не будет искажаться в отличие от реализаций невозможного треугольника в трехмерном пространстве (см.

τέσσαρες ἀκτίνες - четыре луча) - 4-мерный Гиперкуб - аналог в 4-мерном пространстве.

Изображение является проекцией () четырехмерного куба на трехмерное пространство.

Обобщение куба на случаи с числом измерений, большим, чем 3, называется гиперкубом или (en:measure polytopes). Формально гиперкуб определяется как четырёх равных отрезков.

Данная статья в основном описывает 4-мерный гиперкуб , называемый тессеракт .

Популярное описание

Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из нашего трёхмерного .

В одномерном «пространстве» - на линии - выделим АВ длиной L. На двумерной на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат ABCD. Повторив эту операцию с плоскостью, получим трехмерный куб ABCDHEFG. А сдвинув куб в четвёртом измерении (перпендикулярно первым трем!) на расстояние L, мы получим гиперкуб.

Одномерный отрезок АВ служит гранью двумерного квадрата ABCD, квадрат - стороной куба ABCDHEFG, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат - четыре вершины, куб - восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра - по 12 дают начальное и конечное положения исходного куба, и еще 8 ребер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и еще четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани - 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его ребер.

Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб . Воспользуемся для этого уже знакомым методом аналогий.

Возьмем проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями - боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» - трёхмерные грани - будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в четвёртом измерении. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.

Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Ее часть, оставшаяся в «нашем» пространстве, нарисована сплошными линиями, а то, что ушло в гиперпространство, пунктирными. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.

Разрезав восемь граней трёхмерного куба, можно разложить его в плоскую фигуру - развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс еще один - грань, ей противоположную. А трёхмерная развертка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного - конечной «гиперграни».

Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в 4-мерное пространство, представленных в нижеследующей таблице.

Начнём с объяснения, что же такое четырёхмерное пространство.

Это - одномерное пространство, то есть просто ось OX. Любая точка на ней характеризуется одной координатой.

Теперь проведём ось OY перпендикулярно оси OX. Вот и получилось двумерное пространство, то есть плоскость XOY. Любая точка на ней характеризуется двумя координатами - абсциссой и ординатой.

Проведём ось OZ перпендикулярно осям OX и OY. Получится трёхмерное пространство, в котором у любой точки есть абсцисса, ордината и аппликата.

Логично, что четвёртая ось, OQ, должна быть перпендикулярной осям OX, OY и OZ одновременно. Но мы не можем точно построить такую ось, и потому остаётся только попытаться представить её себе. У каждой точки в четырёхмерном пространстве есть четыре координаты: x, y, z и q.

Теперь посмотрим, как появился четырёхмерный куб.

На картинке изображена фигура одномерного пространства - линия.

Если сделать параллельный перенос этой линии вдоль оси OY, а потом соединить соответствующие концы двух получившихся линий, получится квадрат.

Аналогично, если сделать параллельный перенос квадрата вдоль оси OZ и соединить соответствующие вершины, то получится куб.

А если сделать параллельный перенос куба вдоль оси OQ и соединить вершины двух этих кубов, то мы получим четырёхмерный куб. Кстати, он называется тессеракт .

Чтобы нарисовать куб на плоскости, нужно его спроецировать . Наглядно это выглядит так:

Представим, что в воздухе над поверхностью висит каркасная модель куба, то есть как бы «сделанная из проволоки», а над ней - лампочка. Если включить лампочку, обвести карандашом тень от куба, а потом выключить лампочку, то на поверхности будет изображена проекция куба.

Перейдём к немного более сложному. Ещё раз посмотрите на рисунок с лампочкой: как видите, все лучи сошлись в одной точке. Она называется точкой схода и используется для построения перспективной проекции (а бывает и параллельная, когда все лучи параллельны друг другу. Результат - не создаётся ощущения объёма, но она легче, и при том если точка схода достаточно сильно удалена от проецируемого объекта, то разница между этими двумя проекциями мало заметна). Чтобы спроецировать данную точку на данную плоскость, используя точку схода, нужно провести прямую через точку схода и данную точку, а потом найти точку пересечения получившейся прямой и плоскости. А для того, чтобы спроецировать более сложную фигуру, скажем, куб, нужно спроецировать каждую его вершину, а потом соответствующие точки соединить. Следует заметить, что алгоритм проекции пространства на подпространство можно обобщить для случая 4D->3D, а не только 3D->2D.

Как я уже говорил, мы не можем себе точно представить, как выглядит ось OQ, равно как и тессеракт. Зато мы можем получить ограниченное представление о нём, если мы спроецируем его на объём, а потом нарисуем это на экране компьютера!

Теперь поговорим о проекции тессеракта.

Слева находится проекция куба на плоскость, а справа - тессеракта на объём. Они довольно схожи: проекция куба выглядит как два квадрата, маленький и большой, один внутри другого, и у которых соответствующие вершины соединены линиями. А проекция тессеракта выглядит как два куба, маленький и большой, один внутри другого, и у которых соответствующие вершины соединены. Но мы все видели куб, и можем с уверенностью сказать, что и маленький квадрат, и большой, и четыре трапеции сверху, снизу, справа и слева от маленького квадрата, на самом деле являются квадратами, при чём равными. И у тессеракта тоже самое. И большой куб, и маленький куб, и шесть усечённых пирамид по бокам от маленького куба - это всё кубы, при чём равные.

Моя программа умеет не только рисовать проекцию тессеракта на объём, а ещё и вращать его. Рассмотрим, как делается это.

Для начала я вам расскажу, что такое вращение параллельно плоскости .

Представьте себе, что куб вращается вокруг оси OZ. Тогда каждая из его вершин описывает окружность вокруг оси OZ.

А окружность - фигура плоская. И плоскости каждой из этих окружностей параллельны между собой, и в данном случае параллельны плоскости XOY. То есть мы можем говорить не только о вращении вокруг оси OZ, а ещё и о вращении параллельно плоскости XOY.Как видим, у точек, которые вращаются параллельно оси XOY меняются только абсцисса и ордината, аппликата же остаётся неизменной И, вообще-то, мы можем говорить о вращении вокруг прямой только тогда, когда имеем дело с трёхмерным пространством. В двумерном всё вращается вокруг точки, в четырёхмерном - вокруг плоскости, в пятимерном пространстве мы говорим о вращении вокруг объёма. И если вращение вокруг точки мы можем себе представить, то вращение вокруг плоскости и объёма - что-то немыслимое. А если будем говорить о вращении параллельно плоскости, то тогда в любом n-мерном пространстве точка может вращаться параллельно плоскости.

Многие из вас, вероятно, слышали о матрице поворота. Умножив точку на неё, получим точку, повёрнутую параллельно плоскости на угол фи. Для двумерного пространства она выглядит так:

Как умножать: икс точки, повёрнутой на угол фи = косинус угла фи*икс первоначальной точки минус синус угла фи*игрек первоначальной точки;
игрек точки, повёрнутой на угол фи=синус угла фи*икс первоначальной точки плюс косинус угла фи*игрек первоначальной точки.
Xa`=cosф*Xa - sinф*Ya
Ya`=sinф*Xa + cosф*Ya
, где Xa и Ya - абсцисса и ордината точки, которую нужно повернуть, Xa` и Ya` - абсцисса и ордината уже повёрнутой точки

Для трёхмерного пространства это матрица обобщается следующим образом:

Вращение параллельно плоскости XOY. Как видим, координата Z не меняется, а меняются только X и Y
Xa`=cosф*Xa - sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (по сути, Za`=Za)

Вращение параллельно плоскости XOZ. Ничего нового,
Xa`=cosф*Xa + Ya*0 - sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (по сути, Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za

И третья матрица.
Xa`=Xa*1 + Ya*0 + Za*0 (по сути, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya - sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za

А для четвёртого измерения они выглядят вот так:


Думаю, вы уже поняли, что на что множить, потому лишний раз расписывать не буду. Зато замечу, что она делает то же самое, что и матрица для поворота параллельно плоскости в трёхмерном пространстве! И та, и эта изменяют только ординату и аппликату, а остальные координаты не трогают, потому её можно использовать и в трёхмерном случае, просто не обращая внимания на четвёртую координату.

А вот с формулой проекции не всё так просто. Сколько я ни читал форумов, мне не подошёл ни один из способов проекции. Параллельная мне не подходила, так как проекция не будет выглядеть объёмной. В одних формулах проекции для нахождения точки нужно решить систему уравнений(а я не знаю, как научить компьютер их решать), другие я просто-напросто не понял… В общем, я решил придумать свой способ. Рассмотрим для этого проекцию 2D->1D.

pov значит «Point of view» (точка зрения), ptp значит «Point to project» (точка, которую нужно спроецировать), а ptp` - это искомая точка на оси OX.

Углы povptpB и ptpptp`A равны как соответствующие(пунктирная линия параллельна оси OX, прямая povptp - секущая).
Икс точки ptp` равен иксу точки ptp минус длина отрезка ptp`A. Этот отрезок можно найти из треугольника ptpptp`A: ptp`A = ptpA/тангенс угла ptpptp`A. Мы можем найти этот тангенс из треугольника povptpB: тангенс угла ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Ответ: Xptp`=Xptp-Yptp/тангенс угла ptpptp`A.

Я не стал подробно расписывать этот алгоритм тут, так как там куча частных случаев, когда формула несколько меняется. Кому это интересно - посмотрите в исходниках программы, там всё расписано в комментариях.

Для того, чтобы спроецировать точку трёхмерного пространства на плоскость, просто рассмотрим две плоскости - XOZ и YOZ, и для каждой из них решим эту задачу. В случае четырёхмерного пространства нужно рассмотреть уже три плоскости: XOQ, YOQ и ZOQ.

И наконец, про программу. Она действует так: инициализировать шестнадцать вершин тессеракта -> в зависимости от введённых пользователем команд повернуть его -> спроецировать на объём -> в зависимости от введённых пользователем команд повернуть его проекцию -> спроецировать на плоскость -> нарисовать.

Проекции и повороты я написал сам. Они работают по формулам, которые я только что описал. Библиотека OpenGL рисует линии, а так же занимается смешиванием цветов. А координаты вершин тессеракта вычисляются таким образом:

Координаты вершин линии с центром в начале координат и длинной 2 - (1) и (-1);
- " - " - квадрата - " - " - и ребром длинной 2:
(1; 1), (-1; 1), (1; -1) и (-1; -1);
- " - " - куба - " - " -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1), (-1; -1; -1);
Как можно было заметить, квадрат - это одна линия над осью OY и одна линия под осью OY; куб - это один квадрат спереди от плоскости XOY, и один за ней; тессеракт - это один куб по ту сторону объёма XOYZ, и один - по эту. Но куда легче воспринять это чередование единиц и минус единиц, если их записать в столбик

1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1

В первом столбце один и минус один чередуются. Во втором столбце сначала идёт два плюса, потом два минуса. В третьем - четыре плюс единицы, а потом четыре минус единицы. Это были вершины куба. У тессеракта их в два раза больше, и потому нужно было написать цикл для их объявления, иначе очень легко запутаться.

Моя программа так же умеет рисовать анаглиф. Счастливые обладатели 3D-очков могут наблюдать стереоскопическую картинку. В рисовании картинки нет ничего хитрого, просто рисуется две проекции на плоскость, для правого и левого глаз. Зато программа становится намного более наглядной и интересной, а главное - даёт лучшее представление о четырёхмерном мире.

Менее значительные функции - подсветка одной из граней красным, чтобы лучше можно было разглядеть повороты, а так же мелкие удобства - регуляция координат точек-«глаз», увеличение и уменьшение скорости поворота.

Архив с программой, исходником и инструкцией пользования.