Синтез рекурсивных фильтров по аналоговому прототипу

При синтезе стандартных частотно-избирательных фильтров удобно воспользоваться хорошо разработанным аппаратом расчета аналоговых фильтров. Наиболее широкое распространение получили следующие методы:

1. Метод инвариантности импульсной характеристики (метод стандартного - преобразования).

2. Метод билинейного - преобразования.

3. Метод замены производных конечными разностями.

4.2.1. Метод инвариантности импульсной характеристики (метод стандартного - преобразования)

Под инвариантностью импульсной характеристики понимается равенство отсчетов импульсной характеристики цифрового фильтра значениям импульсной характеристики аналогового прототипа, взятым с периодом дискретизации.

Для реализации метода необходимо:

Найти импульсную характеристику прототипа ;

Получить импульсную характеристику цифрового фильтра путем дискретизации с периодом с учетом масштабирующего множителя :

; (4.1)

Найти передаточную функцию фильтра, взяв - преобразование от :

. (4.2)

Рисунок 3.1 – дискретизация импульсной характеристики аналогового прототипа

Предположим, что передаточная функция аналогового прототипа записана в виде суммы простейших дробей:

. (4.3)

В этом случае в соответствии с обратным преобразованием Лапласа импульсная характеристика аналогового прототипа имеет следующий вид:

. (4.4)

После дискретизации получим требуемую импульсную характеристику ЦФ:

Передаточная функция синтезированного цифрового фильтра в результате применения - преобразования имеет следующий вид:

Полученная передаточная функция соответствует параллельной структуре цифрового фильтра. Структурная схема одного звена синтезированного цифрового фильтра с передаточной характеристикой имеет следующий вид: рисунок 3.2.

Рисунок 3.2 – структурная схема одного звена цифрового фильтра

Таким образом, процедура синтеза ЦФ методом инвариантности импульсной характеристики содержит следующие шаги:

1. Задать требования к цифровому фильтру.

3. Разложить на простейшие дроби.

4. Записать передаточную функцию цифрового фильтра на основе соотношений (4.3) и (4.6).

Частотная характеристика полученного фильтра связана с частотной характеристикой аналогового прототипа таким же образом, как спектр дискретизированного сигнала связан со спектром аналогового сигнала: периодическим повторением. Поэтому для получения хороших результатов для данного метода коэффициент передачи аналогового прототипа должен быть пренебрежимо малым на частотах, превышающих частоту Найквиста. Следовательно, метод подходит для создания ФНЧ и ПФ, но неприменим для разработки ФВЧ и РФ.

Пример использования метода инвариантности импульсной характеристики

Пусть передаточная функция аналогового прототипа имеет следующий вид:

.

Таким образом, в соответствии с выражением (4.3) можно записать следующие параметры аналогового прототипа:

,

.

В соответствии с выражением (4.6) получим следующее выражение для передаточной функции искомого цифрового фильтра:

.

Получим уравнение цифровой фильтрации. Для этого запишем передаточную функцию цифрового фильтра в виде:

,

где ,

.

В результате ряда математических преобразований последнего выражения можно получить:

,

После перехода от изображений z-преобразования к оригиналам, получим уравнение цифровой фильтрации:

4.2.2. Метод билинейного - преобразования

Преобразование Лапласа и - преобразование связаны между собой соотношением:

. (4.7)

Выражение (4.7) непосредственно не может быть использовано для расчета цифрового фильтра при известной передаточной характеристике аналогового прототипа, так как обратное соотношение является транцендентным:

. (4.8)

Это затруднение преодолевается использованием разложения в ряд:

.

Используя первый член разложения, можно получить:

. (4.9)

Данное преобразование представляет собой дробно-рациональную функцию первого порядка от аргумента и называется билинейным z – преобразованием .

Передаточная функция цифрового фильтра получается из передаточной функции аналогового прототипа применением следующей замены:

. (4.10)

Рассмотрим свойства билинейного преобразования. Для этого получим:

. (4.11)

Таким образом, билинейное преобразование приводит к существенной деформации АЧХ аналога-прототипа при его пересчете в цифровую форму по сравнению с исходным соотношением . Связь между частотами АЧХ прототипа и частотами цифрового фильтра определяются из соотношения:

.

Окончательно связь между частотой аналогового прототипа и частотой цифрового фильтра имеет следующий вид:

. (4.12)

В соответствии с последним выражением вся ось бесконечная ось АЧХ аналогового прототипа полностью помещается в интервале Найквиста на оси цифровых частот от 0 до : рисунок 3.3. Следовательно, полностью исключается эффект наложения копий частотных характеристик, свойственный методу инвариантности импульсной характеристики. В области малых частот частотные характеристики аналогового и цифрового фильтров совпадают:

. (4.13)

Рисунок 3.3 – трансформация частотной оси при билинейном преобразовании

Эффект деформации АЧХ легко учитывается для частотно-избирательных фильтров, характеризуемых границами полосы пропускания, с использованием последнего выражения связи частот.

Порядок расчета фильтра следующий:

1) АЧХ рассчитываемого фильтра задается в масштабе частот и в этом же масштабе отмечаются характерные точки АЧХ.

2) С помощью преобразующей функции определяются те же характерные точки в масштабе частот для аналогового прототипа и составляется выражение для его передаточной функции .

3) Методом билинейного преобразования передаточная функция пересчитывается в передаточную функцию цифрового фильтра.

Таким образом, устранен недостаток, связанный с деформацией ФЧХ аналогового прототипа.

Метод билинейного преобразования полностью исключает эффект наложения АЧХ, не требует повышения частоты дискретизации для уменьшения ошибок воспроизведения АЧХ. Метод используется, когда не требуется повышенная точность воспроизведения АЧХ аналогового прототипа.

Пример использования метода билинейного преобразования

Пусть передаточная функция аналогового прототипа описывается выражением:

.

С учетом выражения (4.10) можно получить следующее выражение для передаточной функции искомого цифрового фильтра:

,

где ;

Метод инвариантности

Метод инвариантности состоит в том, что в средстве измерений помимо измерительной цепи (канала) имеется сравнительная цепь (канал), к которой не подается входной сигнал, но которая, как и измерительная цепь, находится под воздействием некоторой влияющей величины. Причем параметры сравнительной цепи подобраны так, что изменение ее сигнала под действием влияющей величины идентично изменению сигнала измерительной цепи под действием этой величины, т. е. возмущения, вызванные влияющей величиной, поступают в средство измерений по двум каналам (принцип двухканальности). Использование разности сигналов измерительной и сравнительной цепей (при дифференциальном включении этих цепей) обеспечивает независимость (инвариантность) результирующего сигнала от названной влияющей величины, т. е. метод обеспечивает исключение дополнительной погрешности, вызванной изменениями некоторой, как правило, основной влияющей величины.

Метод прямого хода

Метод прямого хода состоит в том, что измеряемый сигнал поступает к чувствительному элементу средства измерений через ключ, с помощью которого осуществляется периодическое во времени отключение измеряемого сигнала от чувствительного элемента и подача к последнему сигнала, значение которого равно нулю. Это обеспечивает работу средства измерений на восходящей ветви (прямой ход) статической характеристики при всех значениях измеряемого сигнала, что исключает наиболее существенную погрешность многих средств измерений - погрешность от вариации.

Метод вспомогательных измерений

Метод вспомогательных измерений заключается в автоматизации процесса учета дополнительной погрешности средства измерений по известным функциям влияния ряда влияющих величин. Для этого осуществляется измерение значений этих величин и с помощью вычислительного устройства, построенного с учетом названных функций влияния, автоматически корректируется выходной сигнал средства измерений.

Метод обратного преобразования

Метод обратного преобразования (итерационный метод) базируется на использовании дополнительно в составе средства измерений кроме прямой измерительной цепи (прямого преобразователя), цепи, способной осуществлять обратное преобразование выходного сигнала (обратный преобразователь), имеющей существенно большую точность, чем цепь прямого преобразования. Результат измерения получают путем итераций. В процессе каждой итерации последовательно осуществляются: прямое преобразование измеряемой величины и запоминание результата, обратное преобразование запомненного значения этой величины, прямое преобразование сигнала обратного преобразователя, соответствующего запомненному значению измеряемой величины, и сравнение результатов этих двух преобразований, на основе которого формируется корректирующий сигнал. Обратный преобразователь в данном методе играет роль как бы многозначной меры, по которой корректируется статическая характеристика прямого преобразователя. Метод обратного преобразования позволяет уменьшать в зависимости от используемого алгоритма коррекции аддитивную и мультипликативную погрешности средств измерений.

При синтезе дискретного фильтра по аналоговому прототипу необходимо преобразовать функцию передачи аналогового фильтра H(s) в функцию передачи дискретного фильтра H(z). Получающийся дискретный фильтр не может быть полностью идентичен аналоговому по своим характеристикам - хотя бы потому, что частотные характеристики дискретного фильтра являются периодическими. Можно говорить только об определенном соответствии характеристик аналогового и дискретного фильтров. Поскольку теория аппроксимации идеальных АЧХ аналоговыми средствами хорошо развита, методы синтеза дискретных фильтров по аналоговым прототипам получили широкое распространение.

В данном разделе мы рассмотрим два метода синтеза рекурсивных дискретных фильтров по аналоговым прототипам:

Метод инвариантных импульсных характеристик.

В основе этого - простейшего метода синтеза ЦФ лежит предположение о том, что синтезируемый ЦФ должен обладать импульсной характеристикой, которая является результатом дискретизации импульсной характеристики соответствующего аналогового фильтра-прототипа.

Метод инвариантного преобразования ИХ предполагает расчет дискретного фильтра, ИХ которого представляет собой дискретизированную ИХ фильтра-прототипа. Дискретизация временной функции, как известно, приводит к тому, что спектр функции делается периодическим с периодом, равным частоте дискретизации. Поэтому при переходе от непрерывной ИХ к дискретной ИХ частотная характеристика фильтра начинает периодически повторяться со сдвигом, равным частоте дискретизации f 2 . Если частота f 2 установлена достаточно высокой в сравнении с характерными частотами ЧХ фильтра-прототипа, то тогда дискретный фильтр по своим свойствам будет соответствовать непрерывному фильтру-прототипу.

Имея в виду синтез физически реализуемых систем, для которых импульсная характеристика обращается в нуль при t < 0, получим следующее выражение импульсной характеристики ЦФ:

{h k }=(h(0), h(Δ), h(2Δ)) (*)

Следует обратить внимание на то, что число отдельных членов в выражении импульсной характеристики ЦФ может быть как конечным, так и бесконечным. Это определяет структуру синтезируемого фильтра: импульсной характеристике с конечным числом отсчетов отвечает трансверсальный фильтр, в то время как для реализации неограниченно протяженной импульсной характеристики требуется рекурсивный ЦФ.

Частотная характеристика получаемого фильтра связана с частотной характеристикой аналогового прототипа точно так же, как спектр дискретизированного сигнала связан со спектром сигнала аналогового - периодическим повторением. Поэтому для получения хороших результатов при таком методе синтеза коэффициент передачи аналогового прототипа должен быть пренебрежимо малым на частотах, превышающих частоту Найквиста. Отсюда следует также, что этот метод подходит для создания ФНЧ и полосовых фильтров, но непригоден для синтеза ФВЧ и режекторных фильтров.

В качестве примера синтезируем методом инвариантной импульсной характеристики ФНЧ Чебышева 2-го порядка с частотой среза 10 кГц, причем специально выберем недостаточно высокую частоту дискретизации (48 кГц), чтобы хорошо видеть эффекты, связанные с наложением сдвинутых копий спектра (рис. 6.2):

Рис. 6.2. АЧХ аналогового прототипа (пунктир) и дискретного фильтра (сплошная линия), синтезированного методом инвариантной импульсной характеристики

На рисунке хорошо видно, что из-за недостаточно высокой частоты дискретизации коэффициент передачи аналогового фильтра на частоте Найквиста недостаточно мал, что обусловливает заметные искажения формы АЧХ синтезированного дискретного фильтра. Повышение частоты дискретизации позволяет сделать эти искажения пренебрежимо малыми.

Степень приближения амплитудно-частотной характеристики синтезированного ЦФ к характеристике аналогового прототипа зависит от выбранного шага дискретизации Δ . При необходимости следует вычислить частотный коэффициент передачи ЦФ, осуществив в системной функции H(z) замену переменной по формуле z=exp(jωΔ), и затем сравнить результат с частотным коэффициентом передачи аналоговой цепи.

Пример

Рассмотреть синтез трансверсального цифрового фильтра, подобного динамической системе 1-го порядка (например, интегрирующей RC-цепи) с импульсной характеристикой вида

(несущественный для задачи синтеза амплитудный множитель в импульсной характеристике положен равным единице).

Пусть импульсная характеристика апроксимируется последовательностью из трех равноотстоящих отсчетов:

Трансверсальный ЦФ с такой импульсной характеристикой описывается разностным уравнением

Применив z-преобразование к последовательности , находим системную функцию ЦФ

откуда частотный коэффициент передачи

Пример

Рассмотреть случай, когда импульсная характеристика аналоговой цепи аппроксимируется бесконечной дискретной последовательностью

()

Выполнив z-преобразование импульсной характеристики (), получим системную функцию

()

Данной системной функции отвечает рекурсивный ЦФ 1-го порядка, содержащий, помимо сумматора, один масштабный блок и один элемент задержки.

Частотный коэффициент передачи фильтра

Метод инвариантных частотных характеристик (билинейного преобразования).

Принципиально невозможно создать ЦФ, частотная характеристика которого в точности повторяла бы частотную характеристику некоторой аналоговой цепи. Причина состоит в том, что, как известно, частотный коэффициент передачи ЦФ является периодической функцией частоты с периодом, определяемым шагом дискретизации (рис.).

Рис. . Амплитудно-частотные характеристики фильтров:

а - аналогового; 6 - цифрового

Говоря о подобии (инвариантности) частотных характеристик аналогового и цифрового фильтров, можно требовать лишь то, чтобы весь бесконечный интервал частот ω а , относящихся к аналоговой системе, был преобразован в отрезок частот ω ц цифрового фильтра, удовлетворяющих неравенству

-π/Δ<ω ц < π/Δ

при сохранении общего вида АЧХ.

Пусть K а (p) - передаточная функция аналогового фильтра, задаваемая дробно-рациональным выражением по степеням комплексной частоты р . Если воспользоваться связью между переменными z и р:

z = exp(pΔ) ,

то можно записать

p = (1/ Δ) ln z (чч)

Однако с помощью этого закона связи нельзя получить физически реализуемую системную функцию ЦФ, поскольку подстановка (чч) в выражение Ks(p) приведет к системной функции, не выражающейся в виде частного двух многочленов. Требуется найти такую дробно-рациональную функцию от z, которая обладала бы основным свойством преобразования (чч), а именно переводила бы точки единичной окружности, лежащей в плоскости z, в точки мнимой оси на плоскости р.

Среди прочих способов для синтеза фильтров нижних частот получила распространение связь вида

устанавливающая однозначное соответствие между точками единичной окружности в z-плоскости со всей мнимой осью в р-плоскости. Характерная особенность этого закона преобразования состоит в следующем. Пусть в (15.97) выполнена замена переменной

z = exp(j ω ц Δ), .

откуда вытекает соотношение между частотными переменными соа и соц аналоговой и цифровой систем:

(15.98)

Если частота дискретизации достаточно велика (ω ц Δ <<1), то, как легко видеть из формулы (15.98), . Таким образом, на низких частотах характеристики аналогового и цифрового фильтров практически совпадают. В общем случае нужно принимать во внимание трансформацию масштаба по оси частот цифрового фильтра, описываемого формулой (15.98).

Практически процедура синтеза ЦФ состоит в том, что в функции Кл(р) аналоговой цепи выполняется замена переменной по формуле (15.97). Полученная при этом системная функция ЦФ оказывается дробно-рациональной и поэтому позволяет непосредственно записать алгоритм цифровой фильтрации.

Пример

Синтезировать цифровой фильтр с частотной характеристикой, подобной характеристике аналогового ФНЧ. Частота среза для ЦФ ω сц = 1500 с -1 . Частота дискретизации ω д = 10000 с -1 .

Прежде всего определяем шаг дискретизации

Для получения дискретного фильтра с заданными частотами среза необходимо скорректировать частоты среза аналогового прототипа, чтобы компенсировать искажения частотной оси. Так, для синтеза дискретного ФНЧ с частотой среза се>од аналоговый фильтр-прототип должен иметь частоту среза Юо а, связанную с со 0 д следующим образом:

По формуле (15.98) находим частоту среза аналогового фильтра, подобного синтезируемому ЦФ:

Передаточная функция аналогового ФНЧ

К а (р)

Выполнив в замену переменной вида (15.97), находим системную функцию ЦФ:

Рис. 60. Амплитудно-частотные характеристики фильтра-прототипа (1} и синтезированных БИХ-фильтров (2-5)

Сравнивая кривые 1 и 2, видим, что наложение спектров, характерное для дискретного фильтра(инвар мет), приводит к ухудшению вида АЧХ фильтра в сравнении с фильтром-прототипом. Однако это ухудшение будет тем меньше, чем больше отношение частоты дискретизации f 2 =1/T 2 к частоте среза фильтра f c . В данном случае f 2 /fс=10 . Если, например, выбрать f 2 /f c =20 , то тогда получим для дискретного фильтра АЧХ, представленную кривой 3 на рис. 60. Эта кривая заметно ближе к кривой 1 (АЧХ фильтра-прототипа), чем кривая 2.

Из сравнения АЧХ дискретного БИХ-фильтра, рассчитанного методом инвариантного преобразования ИХ (кривые 2 и 3 на рис. 60), и БИХ-фильтра, найденного методом билинейного преобразования (кривая 4), видно, что второй метод дает меньшие значения АЧХ в полосе заграждения. Это объясняется отсутствием здесь эффекта наложения спектров, характерного для метода инвариантного преобразования ИХ.

Вместе с тем сравнение кривых 1 и 4 на рис. 60 дает основание сделать вывод, что метод билинейного преобразования приводит к некоторому изменению масштаба по оси частот: у дискретного фильтра спад АЧХ наступает раньше, чем у непрерывного фильтра-прототипа. Соотношение между частотой f непрерывного фильтра и частотой f n дискретного фильтра можно найти из равенства (330)

Итак, метод инвариантного преобразования импульсной характеристики сохраняет масштаб графика АЧХ по горизонтальной оси (оси частот), но дает искажения по вертикальной оси вследствие эффекта наложения. Что же касается метода билинейного преобразования, то здесь картина обратная: по вертикальной оси график не искажается, но происходит деформация графика на горизонтальной оси. Зная характер этой деформации, можно заранее внести соответствующие изменения в ЧХ фильтра-прототипа для того, чтобы получить желаемый результат.

Муниципальное бюджетное общеобразовательное учреждение гимназия № 9

ЭКСПЕРИМЕНТАЛЬНО-РЕФЕРАТИВНЫЙ ПРОЕКТ

по теме:

Применение метода инвариантов при решении задач ЕГЭ и олимпиадных задач

Выполнила:

ученица XI «Б» класса

Тищенко Элина

Научный руководитель:

учитель математики

Хатунцева

Ирина Владимировна

Воронеж – 2017

Содежание

Введение

В современной математике важную роль играет понятие инвариантности, т.е. неизменность математического объекта. Очень многие определения математики фактически связаны с этим понятием, хотя сам термин инвариантности в учебниках отсутствует.

Пример: четная функция f(x) с областью определения R инвариантна, т.к. f(x)= f(-x).

Наличие того или иного свойства инвариантности у математического объекта позволяет установить некоторые общие качественные свойства этого объекта.

Цель данной работы - показать применение метода инвариантов при решении задач ЕГЭ и олимпиадных задач.

Этой теме посвящено много литературы издательств ведущих ВУЗов страны, таких как МГУ и МФТИ. Классической книгой по теории инвариантов является книга выдающегося немецкого математика Герлеана Вейля. А студентами Оксфордского Университета издается ежегодный журнал "The Invariant".

Эта тема представляется очень актуальной, т.к. метод инвариантов позволяет довольно просто решать задачи повышенного уровня сложности.

Глава 1. Применение метода инварианто в при решении олимпиадных задач

В качестве инварианта чаще всего рассматриваются четность (нечетность), остаток от деления, перестановки, раскраски и т.д.

Применение четности – одна из наиболее часто встречающихся идей при решении олимпиадных задач. Сформулируем наиболее важные утверждения, на которых основано применение этой идеи:

четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых;

знак произведения нескольких (отличных от нуля) чисел определяется четностью количества отрицательных сомножителей.

Задача 1.

На доске написано десять плюсов и пятнадцать минусов. Разрешается стереть любые два знака и написать вместо них плюс, если они одинаковы, и минус в противном случае. Какой знак останется на доске после выполнения двадцати четырех таких операций?

Решение.

Заменим каждый плюс числом 1 , а каждый минус числом -1 .

Тогда мы стираем любые два числа и записываем их произведение. Поэтому произведение всех написанных на доске чисел останется неизменным.

Так как произведение изначально было отрицательным (15 отрицательных чисел), то и в конце оно останется отрицательным .

Ответ: минус.

Задача 2.

Мальчик получил двойку за контрольную работу по математике и в порыве отчаяния разорвал листок со своей работой на десять кусков. Затем один из получившихся кусков он разорвал еще на 10 кусков. Может ли по завершении релаксации оказаться 2015 кусков бумаги?

Решение.

Каждый раз при разрывании одного куска бумаги на 10, мальчик увеличивает общее количество кусков бумаги на 9. После первого разрывания у него будет 1+9=10 кусков, после второго – 10+9=19 кусков и т.д. Т.е., количество кусков бумаги на n-ном разрывании находится по формуле 1+9 n .

Проверим, представимо ли число 2015 в виде 1+9 n :

1+9 n =2015;

9 n =2014.

2014 не делится на 9 без остатка, следовательно, 2015 кусков по завершении релаксации оказаться не может.

Ответ: нет

Задача 3.

На доске записаны числа от 1 до 1998. Разрешается за один ход стирать любые два числа и вместо них записывать их разность, пока не останется одно число. Может ли это число быть нулем?

Решение.

Рассмотрим сумму всех чисел, записанных на доске до и после одного шага. Пусть мы стерли числа a , b . Тогда сначала сумма всех чисел была равна , а потом , где S – сумма всех остальных чисел. Как видим, замена (a + b ) на ( a - b ) не меняет четности суммы всех чисел. Сумма чисел в самом начале есть нечетное число (
), значит, на каждом шаге сумма записанных на доске чисел будет нечетна. Ноль – четное число, поэтому получить его на доске мы не можем.

Ответ: нет.

Задача 4.

Каждая клетка квадратной таблицы 2*2 закрашена в черный или белый цвет, как показано на рисунке ниже. За один ход можно перекрасить клетки в любой строке, в любом столбце или в любой диагонали: черные – в белый цвет, а белые – в черный. Можно ли через несколько ходов получить таблицу, все клетки которой белые?

Решение.

Сопоставим каждой клетке 1, если она покрашена в белый цвет, и -1, если она покрашена в черный цвет. Тогда смена цветов означает смену знаков. Рассмотрим произведение всех чисел, соответствующих клеткам. Так как при перекрашивании мы изменяем знаки ровно у двух сомножителей, то произведение всех четырех чисел не изменяется. В самом начале это произведение равно -1. Требуемой раскраске соответствует произведение, равное 1. Следовательно, указанными операциями перекрасить таблицу невозможно.

Ответ: нет.

Задача 5.

В трех кучках лежат 1, 9 и 98 камней. За один ход разрешается из любых двух кучек взять по одному камню и переложить их в третью. Можно ли за несколько ходов собрать все камни в одной из кучек?

Решение.

Рассмотрим остатки при делении на три исходных чисел – количества камней в кучках. В первой кучке остаток 1, во второй – 0, в третьей – 2. Рассмотрим, что будет дальше происходить с точки зрения остатков, когда мы перекладываем камни:

Мы нашли инвариант – после любой из операций остатки будут прежние: 0, 1, 2, только уже распределены по-другому. Если же мы сможем собрать все камни в одной кучке, то остатки при делении на 3 во всех кучках будет одинаковые (равны 0). Следовательно, указанными операциями собрать все камни в одной кучке нельзя.

Ответ: нет.

Задача 6.

На плоскости дана несамопересекающаяся замкнутая ломаная, никакие три вершины которой не лежат на одной прямой. Назовем пару несоседних звеньев ломаной особой, если продолжение одного из них пересекает другое. Докажите, что число особых пар чётно.

Решение.

Возьмем соседние звенья АВ и ВС и назовем уголком угол, симметричный углу АВС относительно точки В (на рисунке ниже уголок заштрихован). Такие же уголки можно рассмотреть для всех вершин ломаной. Ясно, что число особых пар равно числу точек пересечения звеньев с уголками. Остается заметить, что число звеньев ломаной, пересекающихся с одним уголком, четно, т.к. по пути от А к С ломаная входит в уголок столько же раз, сколько выходит из него (это следует из условия, что никакие три вершины ломаной не лежат на одной прямой). Следовательно, число особых пар чётно, что и требовалось доказать.

Задача 7 (региональный этап Всероссийской олимпиады школьников, 2016-2017 г.г., 11 класс, второй день, №8).

Изначально на стол кладут 100 карточек, на каждой из которых записано по натуральному числу; при этом среди них ровно 28 карточек с нечётными числами. Затем каждую минуту проводится следующая процедура. Для каждых 12 карточек, лежащих на столе, вычисляется произведение записанных на них чисел, все эти произведения складываются, и полученное число записывается на новую карточку, которая добавляется к лежащим на столе. Можно ли выбрать исходные 100 чисел так, что для любого натурального d на столе рано или поздно появится карточка с числом, делящимся на
?

Решение.

Если в некоторый момент среди чисел на карточках есть ровно k нечётных, то среди произведений чисел по 12 ровно
нечётных; поэтому число на очередной добавляемой карточке будет нечётным ровно тогда, когда нечётно (и тогда k в эту минуту увеличится на 1).

Нетрудно заметить, что число
нечётно (это следует из того, что степени двойки, входящие в
и
, равны). Далее, при последовательной проверке получаем, что первое
,
,
- нечетные числа, а
- четное. Следовательно, когда количество нечетных карточек достигнет 32, больше оно увеличиваться не будет, и на столе всегда будет лежать только 32 нечетные карточки, а все добавляемые числа будут четными.

Пусть теперь на n -ном шаге – сумма всех произведений по 12 из чисел, написанных на карточках, а – сумма всех произведений по 11 чисел. Число
, которое будет записано на следующей карточке, отличается от на сумму произведений по 12 чисел, среди которых есть только что добавленное четное число , т.е. на
. Значит, . Число - четное, так как количество нечетных сумм по 11
четно. Значит,
нечетно, и максимальная степень двойки, на которую делится
равна максимальной степени двойки, на которую делится . Значит, так как изначально на столе не лежали числа, которые для любого натурального d делились на , то и дальше такие числа не появятся.

Ответ: нет, нельзя.

Глава 2. Применение метода инвариантов в задах ЕГЭ, содержащих параметр

После анализа большого количества задач, был составлен алгоритм решения задач с параметром методом инвариантов..

Алгоритм решения задач с параметрами с помощью инварианта:

1) проверить на инвариантность данное уравнение, неравенство, систему уравнений (неравенств);

2) найти допустимые значения параметра из проверки выполнения условий: при «симметрии относительно знака переменной» подставить её нулевое значение; при «симметрии относительно перестановки переменных» все переменные обозначают одной буквой;

3) проверкой убедиться, что найденные значения параметра удовлетворяют условию задачи;

4) записать ответ.

Утверждение 1 . Если выражение
инвариантно относительно преобразования
и уравнение
имеет корень ,то

Утверждение 2. Если выражение

и уравнение
имеет решение
, то и пара чисел

Утверждение 3 . Если выражение
инвариантно относительно преобразования
и уравнение
имеет решение
, то и пара чисел
также решение этого уравнения.

Утверждение 4. Если выражение
инвариантно относительно преобразования
и
, а уравнение
имеет решение
, то и пара чисел
также решение этого уравнения.

Утверждение 5. Если выражение
инвариантно относительно преобразования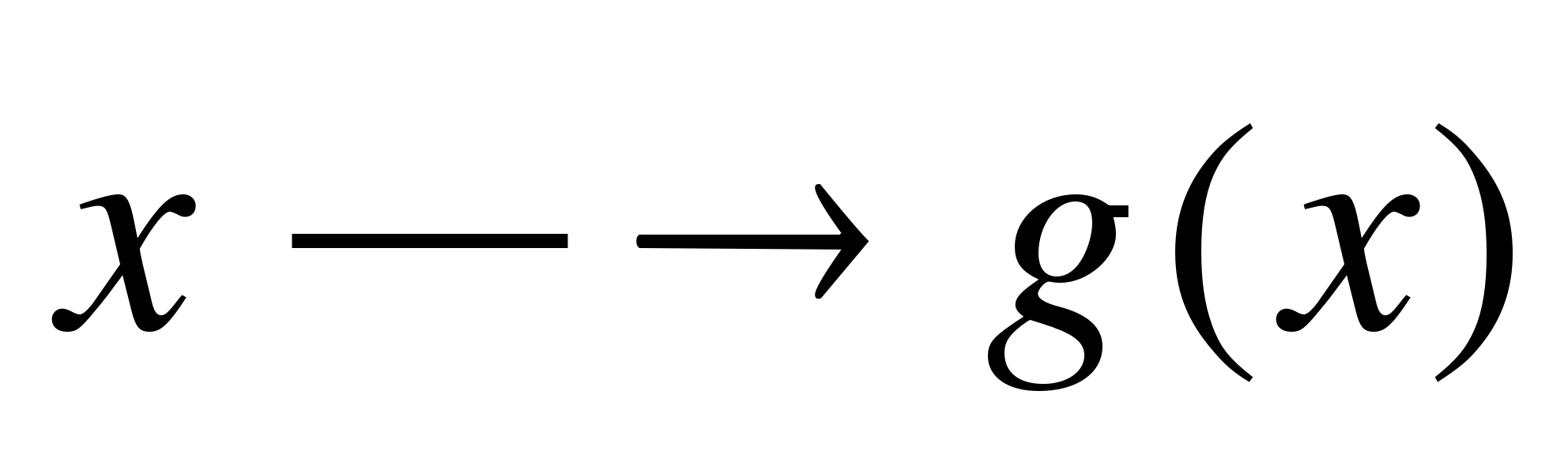
, уравнение
имеет корень , то
также корень этого уравнения.

Задача 1.

Найти все значения параметра а, при которых уравнение имеет одно решение

Решение.

Заметим, что если является корнем уравнения, то - - тоже корень => один корень может быть только если =-=0.
Подставим
:

При
:

1 корень, подходит

При
:

Левая часть этого уравнения больше или равна
, причем эта нижняя граница является точной – она достигается при
. Оценить правую часть немного сложнее. Прежде всего отметим, что при изменении переменной от
до
выражение
меняется от -1 до 1. На отрезке
функция
монотонно возрастает от
до
. Поэтому выражение
меняется от
до
. Соответственно, правая часть уравнения (1) меняется от
до
, причем значения правой части уравнения полностью заполняют этот отрезок. Из полученной информации относительно возможных значений левой и правой частей уравнения (1) следует, что они могут быть равны только тогда, когда одновременно равны
. Иначе говоря, уравнение (1) равносильно системе:

Первое уравнение имеет единственный корень
, который удовлетворяет и второму уравнению системы. Значит, система, а вместе с ней и исходное уравнение имеет единственное решение
. Поэтому проверяемое значение параметра (
) нужно включить в ответ задачи.

Ответ: 0;
.

Задача 2. система неравенств
имеет единственное решение?

Решение. 1. В данной системе наблюдаем «симметрию относительно замены переменных». Тогда, если –решение системы, то и
также решение системы. Единственность решения достигается при условии
(Утверждение 4).

2. Обозначив все переменные через
Из неравенства которое имеет единственное решение, если дискриминант квадратного трёхчлена равен нулю, т.е.

3. Проверим, имеет ли система единственное решение при найденных значениях параметра.

а) Подставим в данную систему неравенств
:

Сложим неравенства последней системы:
+

Раскрыв скобки и приведя подобные слагаемые, получим: . Отсюда



- единственное решение.

б) При подстановке
получим единственное решение

Ответ:

Задача 3. Найдите все значения параметра , при которых система уравнений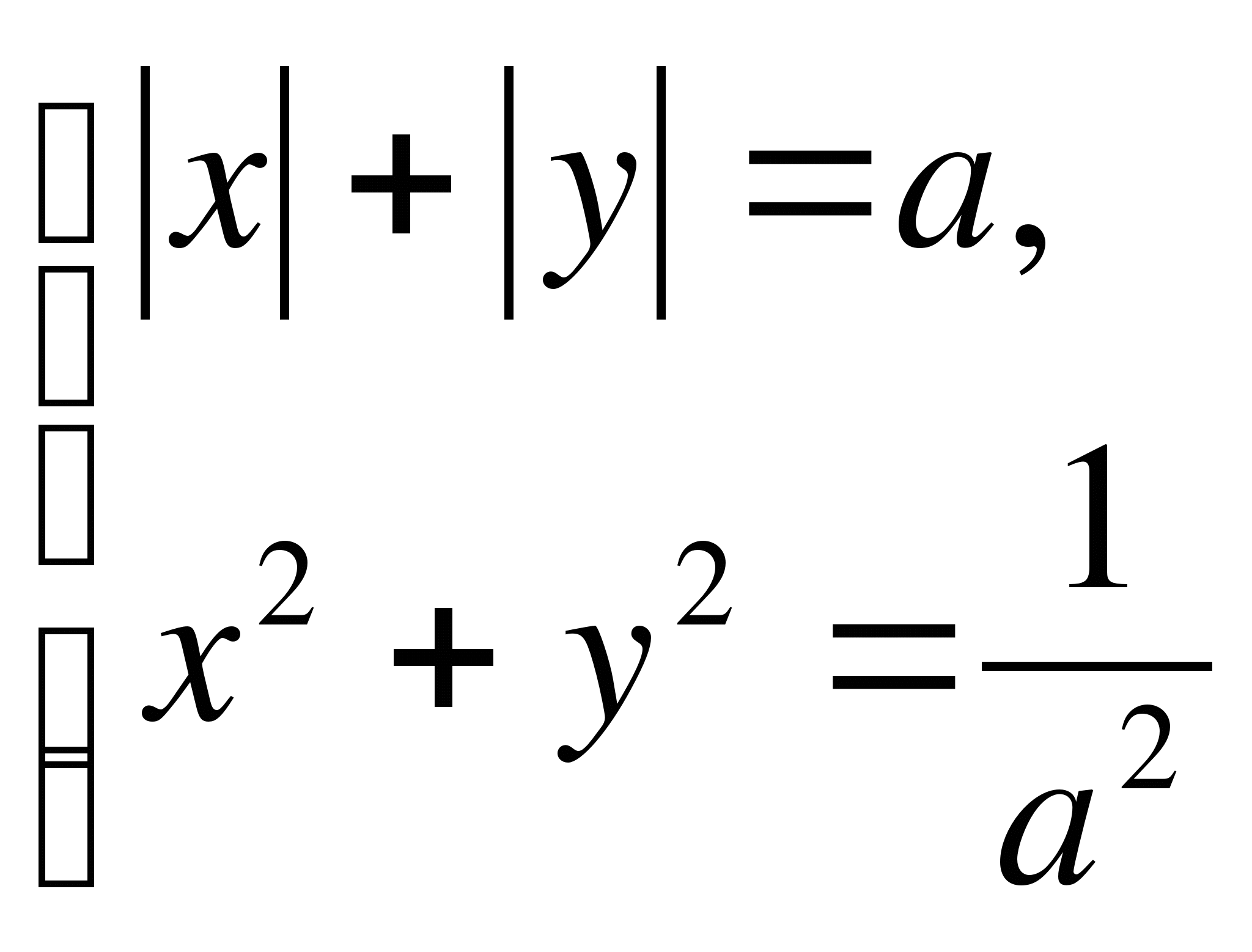

имеет четыре различных решения.

Решение.

Из вида системы следует, что> 0.

1.Система инвариантна при замене на - и на -. Поэтому, если искомое значение параметра и пара чисел ;
- решение системы, то пары
;
, ;
и
; -
также решения системы. (Утверждения 2 и 3). Поэтому найдем решения при ≥ 0, ≥0. Изобразим графики уравнений в одной системе координат. График первого уравнения – точки сторон квадрата ABCD , график второго - окружность с центром в начале координат и радиусом, равным .

По рисунку видно, что система имеет ровно четыре решения в двух случаях: 1)


;
; так как > 0, то
; 2) = 0 E - радиус окружности, вписанной в квадрат, сторона которого равна
по т. Пифагора из треугольника ВОС.

Значит, 0Е =
, тогда =
откуда 2
= 2; 2 =
и =
.

Ответ: = 1; =
.

Задача 4. При каких значениях параметра система уравнений
имеет ровно три решения?

Решение. 1. Если пара чисел ;
– решение системы, - искомый параметр, то пара

; -
– также решение системы. Значит, = -
= 0.(Утверждение 3).

2.Подставим = 0 в данную систему уравнений.

Получим:

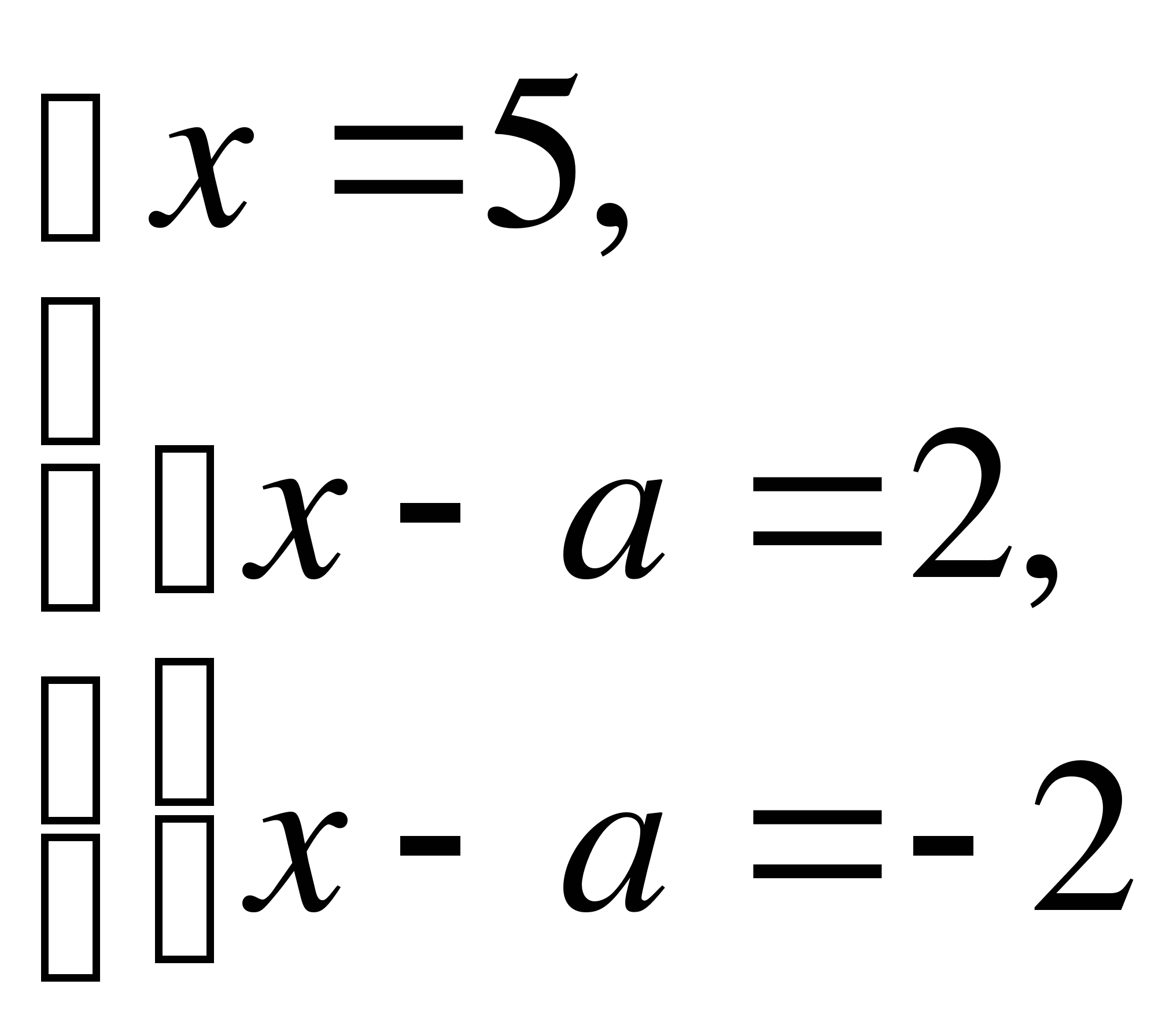
Проверим, имеет ли данное уравнение при найденных значениях единственное решение. При =-3 имеем:

Решим второе уравнение системы:

или
не имеет решений.

Если у=0, то х=5 и (-5; 0) – единственное решение системы. Значит,
не подходит. . Заключение

В ходе проделанной работы был изучен метод инвариантов. Был применён метод инвариантов при решении задач ЕГЭ, содержащих параметр, и олимпиадных задач на раскраску, четность, остатки от деления, обосновано и наглядно показано практическое применение метода.

Список использованной литературы