Муниципальное бюджетное общеобразовательное учреждение гимназия № 9

ЭКСПЕРИМЕНТАЛЬНО-РЕФЕРАТИВНЫЙ ПРОЕКТ

по теме:

Применение метода инвариантов при решении задач ЕГЭ и олимпиадных задач

Выполнила:

ученица XI «Б» класса

Тищенко Элина

Научный руководитель:

учитель математики

Хатунцева

Ирина Владимировна

Воронеж – 2017

Содежание

Введение

В современной математике важную роль играет понятие инвариантности, т.е. неизменность математического объекта. Очень многие определения математики фактически связаны с этим понятием, хотя сам термин инвариантности в учебниках отсутствует.

Пример: четная функция f(x) с областью определения R инвариантна, т.к. f(x)= f(-x).

Наличие того или иного свойства инвариантности у математического объекта позволяет установить некоторые общие качественные свойства этого объекта.

Цель данной работы - показать применение метода инвариантов при решении задач ЕГЭ и олимпиадных задач.

Этой теме посвящено много литературы издательств ведущих ВУЗов страны, таких как МГУ и МФТИ. Классической книгой по теории инвариантов является книга выдающегося немецкого математика Герлеана Вейля. А студентами Оксфордского Университета издается ежегодный журнал "The Invariant".

Эта тема представляется очень актуальной, т.к. метод инвариантов позволяет довольно просто решать задачи повышенного уровня сложности.

Глава 1. Применение метода инварианто в при решении олимпиадных задач

В качестве инварианта чаще всего рассматриваются четность (нечетность), остаток от деления, перестановки, раскраски и т.д.

Применение четности – одна из наиболее часто встречающихся идей при решении олимпиадных задач. Сформулируем наиболее важные утверждения, на которых основано применение этой идеи:

четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых;

знак произведения нескольких (отличных от нуля) чисел определяется четностью количества отрицательных сомножителей.

Задача 1.

На доске написано десять плюсов и пятнадцать минусов. Разрешается стереть любые два знака и написать вместо них плюс, если они одинаковы, и минус в противном случае. Какой знак останется на доске после выполнения двадцати четырех таких операций?

Решение.

Заменим каждый плюс числом 1 , а каждый минус числом -1 .

Тогда мы стираем любые два числа и записываем их произведение. Поэтому произведение всех написанных на доске чисел останется неизменным.

Так как произведение изначально было отрицательным (15 отрицательных чисел), то и в конце оно останется отрицательным .

Ответ: минус.

Задача 2.

Мальчик получил двойку за контрольную работу по математике и в порыве отчаяния разорвал листок со своей работой на десять кусков. Затем один из получившихся кусков он разорвал еще на 10 кусков. Может ли по завершении релаксации оказаться 2015 кусков бумаги?

Решение.

Каждый раз при разрывании одного куска бумаги на 10, мальчик увеличивает общее количество кусков бумаги на 9. После первого разрывания у него будет 1+9=10 кусков, после второго – 10+9=19 кусков и т.д. Т.е., количество кусков бумаги на n-ном разрывании находится по формуле 1+9 n .

Проверим, представимо ли число 2015 в виде 1+9 n :

1+9 n =2015;

9 n =2014.

2014 не делится на 9 без остатка, следовательно, 2015 кусков по завершении релаксации оказаться не может.

Ответ: нет

Задача 3.

На доске записаны числа от 1 до 1998. Разрешается за один ход стирать любые два числа и вместо них записывать их разность, пока не останется одно число. Может ли это число быть нулем?

Решение.

Рассмотрим сумму всех чисел, записанных на доске до и после одного шага. Пусть мы стерли числа a , b . Тогда сначала сумма всех чисел была равна , а потом , где S – сумма всех остальных чисел. Как видим, замена (a + b ) на ( a - b ) не меняет четности суммы всех чисел. Сумма чисел в самом начале есть нечетное число (
), значит, на каждом шаге сумма записанных на доске чисел будет нечетна. Ноль – четное число, поэтому получить его на доске мы не можем.

Ответ: нет.

Задача 4.

Каждая клетка квадратной таблицы 2*2 закрашена в черный или белый цвет, как показано на рисунке ниже. За один ход можно перекрасить клетки в любой строке, в любом столбце или в любой диагонали: черные – в белый цвет, а белые – в черный. Можно ли через несколько ходов получить таблицу, все клетки которой белые?

Решение.

Сопоставим каждой клетке 1, если она покрашена в белый цвет, и -1, если она покрашена в черный цвет. Тогда смена цветов означает смену знаков. Рассмотрим произведение всех чисел, соответствующих клеткам. Так как при перекрашивании мы изменяем знаки ровно у двух сомножителей, то произведение всех четырех чисел не изменяется. В самом начале это произведение равно -1. Требуемой раскраске соответствует произведение, равное 1. Следовательно, указанными операциями перекрасить таблицу невозможно.

Ответ: нет.

Задача 5.

В трех кучках лежат 1, 9 и 98 камней. За один ход разрешается из любых двух кучек взять по одному камню и переложить их в третью. Можно ли за несколько ходов собрать все камни в одной из кучек?

Решение.

Рассмотрим остатки при делении на три исходных чисел – количества камней в кучках. В первой кучке остаток 1, во второй – 0, в третьей – 2. Рассмотрим, что будет дальше происходить с точки зрения остатков, когда мы перекладываем камни:

Мы нашли инвариант – после любой из операций остатки будут прежние: 0, 1, 2, только уже распределены по-другому. Если же мы сможем собрать все камни в одной кучке, то остатки при делении на 3 во всех кучках будет одинаковые (равны 0). Следовательно, указанными операциями собрать все камни в одной кучке нельзя.

Ответ: нет.

Задача 6.

На плоскости дана несамопересекающаяся замкнутая ломаная, никакие три вершины которой не лежат на одной прямой. Назовем пару несоседних звеньев ломаной особой, если продолжение одного из них пересекает другое. Докажите, что число особых пар чётно.

Решение.

Возьмем соседние звенья АВ и ВС и назовем уголком угол, симметричный углу АВС относительно точки В (на рисунке ниже уголок заштрихован). Такие же уголки можно рассмотреть для всех вершин ломаной. Ясно, что число особых пар равно числу точек пересечения звеньев с уголками. Остается заметить, что число звеньев ломаной, пересекающихся с одним уголком, четно, т.к. по пути от А к С ломаная входит в уголок столько же раз, сколько выходит из него (это следует из условия, что никакие три вершины ломаной не лежат на одной прямой). Следовательно, число особых пар чётно, что и требовалось доказать.

Задача 7 (региональный этап Всероссийской олимпиады школьников, 2016-2017 г.г., 11 класс, второй день, №8).

Изначально на стол кладут 100 карточек, на каждой из которых записано по натуральному числу; при этом среди них ровно 28 карточек с нечётными числами. Затем каждую минуту проводится следующая процедура. Для каждых 12 карточек, лежащих на столе, вычисляется произведение записанных на них чисел, все эти произведения складываются, и полученное число записывается на новую карточку, которая добавляется к лежащим на столе. Можно ли выбрать исходные 100 чисел так, что для любого натурального d на столе рано или поздно появится карточка с числом, делящимся на
?

Решение.

Если в некоторый момент среди чисел на карточках есть ровно k нечётных, то среди произведений чисел по 12 ровно
нечётных; поэтому число на очередной добавляемой карточке будет нечётным ровно тогда, когда нечётно (и тогда k в эту минуту увеличится на 1).

Нетрудно заметить, что число
нечётно (это следует из того, что степени двойки, входящие в
и
, равны). Далее, при последовательной проверке получаем, что первое
,
,
- нечетные числа, а
- четное. Следовательно, когда количество нечетных карточек достигнет 32, больше оно увеличиваться не будет, и на столе всегда будет лежать только 32 нечетные карточки, а все добавляемые числа будут четными.

Пусть теперь на n -ном шаге – сумма всех произведений по 12 из чисел, написанных на карточках, а – сумма всех произведений по 11 чисел. Число
, которое будет записано на следующей карточке, отличается от на сумму произведений по 12 чисел, среди которых есть только что добавленное четное число , т.е. на
. Значит, . Число - четное, так как количество нечетных сумм по 11
четно. Значит,
нечетно, и максимальная степень двойки, на которую делится
равна максимальной степени двойки, на которую делится . Значит, так как изначально на столе не лежали числа, которые для любого натурального d делились на , то и дальше такие числа не появятся.

Ответ: нет, нельзя.

Глава 2. Применение метода инвариантов в задах ЕГЭ, содержащих параметр

После анализа большого количества задач, был составлен алгоритм решения задач с параметром методом инвариантов..

Алгоритм решения задач с параметрами с помощью инварианта:

1) проверить на инвариантность данное уравнение, неравенство, систему уравнений (неравенств);

2) найти допустимые значения параметра из проверки выполнения условий: при «симметрии относительно знака переменной» подставить её нулевое значение; при «симметрии относительно перестановки переменных» все переменные обозначают одной буквой;

3) проверкой убедиться, что найденные значения параметра удовлетворяют условию задачи;

4) записать ответ.

Утверждение 1 . Если выражение
инвариантно относительно преобразования
и уравнение
имеет корень ,то

Утверждение 2. Если выражение

и уравнение
имеет решение
, то и пара чисел

Утверждение 3 . Если выражение
инвариантно относительно преобразования
и уравнение
имеет решение
, то и пара чисел
также решение этого уравнения.

Утверждение 4. Если выражение
инвариантно относительно преобразования
и
, а уравнение
имеет решение
, то и пара чисел
также решение этого уравнения.

Утверждение 5. Если выражение
инвариантно относительно преобразования
, уравнение
имеет корень , то
также корень этого уравнения.

Задача 1.

Найти все значения параметра а, при которых уравнение имеет одно решение

Решение.

Заметим, что если является корнем уравнения, то - - тоже корень => один корень может быть только если =-=0.
Подставим
:

При
:

1 корень, подходит

При
:

Левая часть этого уравнения больше или равна
, причем эта нижняя граница является точной – она достигается при
. Оценить правую часть немного сложнее. Прежде всего отметим, что при изменении переменной от
до
выражение
меняется от -1 до 1. На отрезке
функция
монотонно возрастает от
до
. Поэтому выражение
меняется от
до
. Соответственно, правая часть уравнения (1) меняется от
до
, причем значения правой части уравнения полностью заполняют этот отрезок. Из полученной информации относительно возможных значений левой и правой частей уравнения (1) следует, что они могут быть равны только тогда, когда одновременно равны
. Иначе говоря, уравнение (1) равносильно системе:

Первое уравнение имеет единственный корень
, который удовлетворяет и второму уравнению системы. Значит, система, а вместе с ней и исходное уравнение имеет единственное решение
. Поэтому проверяемое значение параметра (
) нужно включить в ответ задачи.

Ответ: 0;
.

Задача 2. система неравенств
имеет единственное решение?

Решение. 1. В данной системе наблюдаем «симметрию относительно замены переменных». Тогда, если –решение системы, то и
также решение системы. Единственность решения достигается при условии
(Утверждение 4).

2. Обозначив все переменные через
Из неравенства которое имеет единственное решение, если дискриминант квадратного трёхчлена равен нулю, т.е.

3. Проверим, имеет ли система единственное решение при найденных значениях параметра.

а) Подставим в данную систему неравенств
:

Сложим неравенства последней системы:
+

Раскрыв скобки и приведя подобные слагаемые, получим: . Отсюда



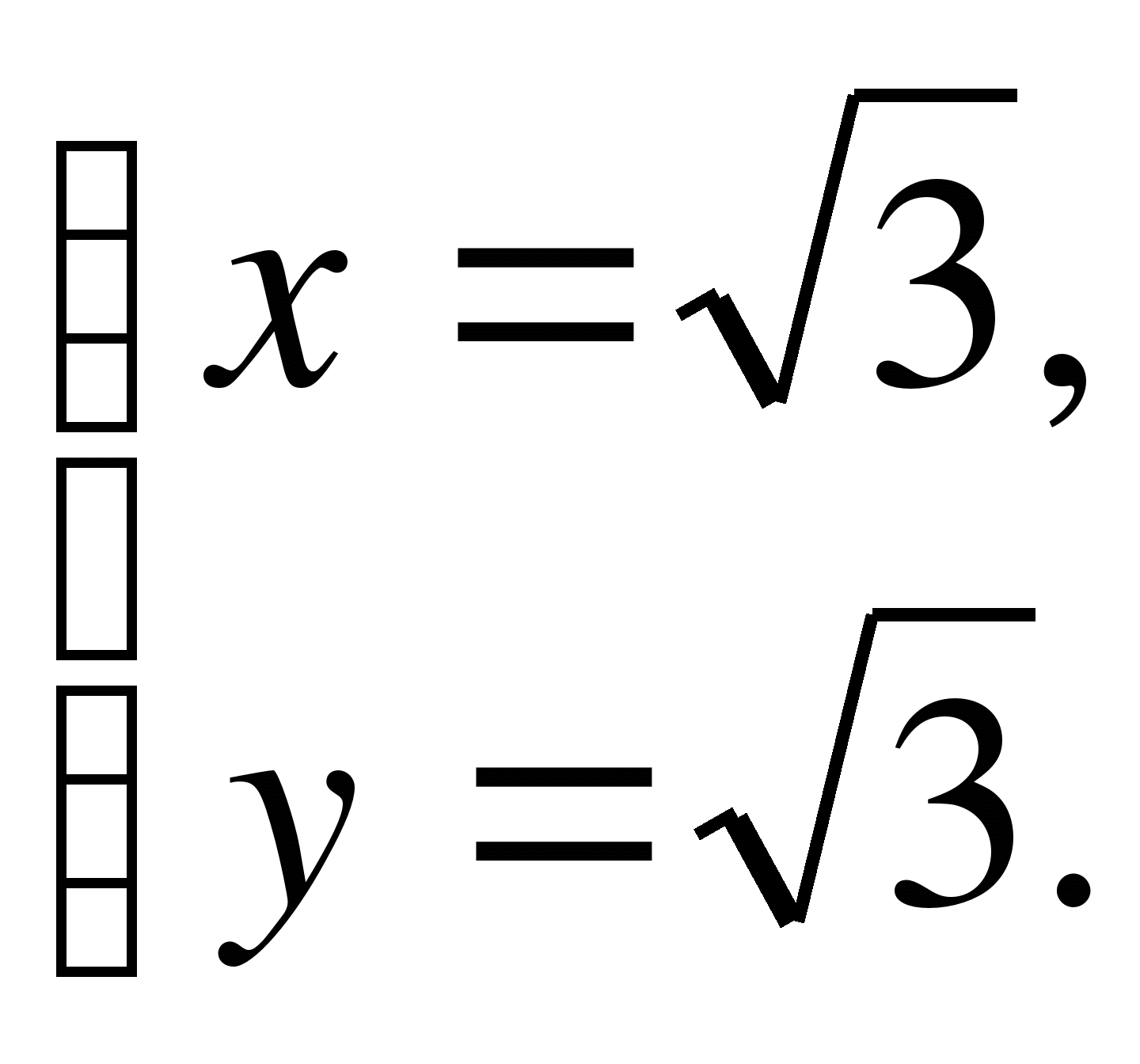- единственное решение.

б) При подстановке
получим единственное решение

Ответ:

Задача 3. Найдите все значения параметра , при которых система уравнений

имеет четыре различных решения.

Решение.

Из вида системы следует, что> 0.

1.Система инвариантна при замене на - и на -. Поэтому, если искомое значение параметра и пара чисел ;
- решение системы, то пары
;
, ;
и
; -
также решения системы. (Утверждения 2 и 3). Поэтому найдем решения при ≥ 0, ≥0. Изобразим графики уравнений в одной системе координат. График первого уравнения – точки сторон квадрата ABCD , график второго - окружность с центром в начале координат и радиусом, равным .

По рисунку видно, что система имеет ровно четыре решения в двух случаях: 1)


;
; так как > 0, то
; 2) = 0 E - радиус окружности, вписанной в квадрат, сторона которого равна
по т. Пифагора из треугольника ВОС.

Значит, 0Е =
, тогда =
откуда 2
= 2; 2 =
и =
.

Ответ: = 1; =
.

Задача 4. При каких значениях параметра система уравнений
имеет ровно три решения?

Решение. 1. Если пара чисел ;
– решение системы, - искомый параметр, то пара

; -
– также решение системы. Значит, = -
= 0.(Утверждение 3).

2.Подставим = 0 в данную систему уравнений.

Получим:

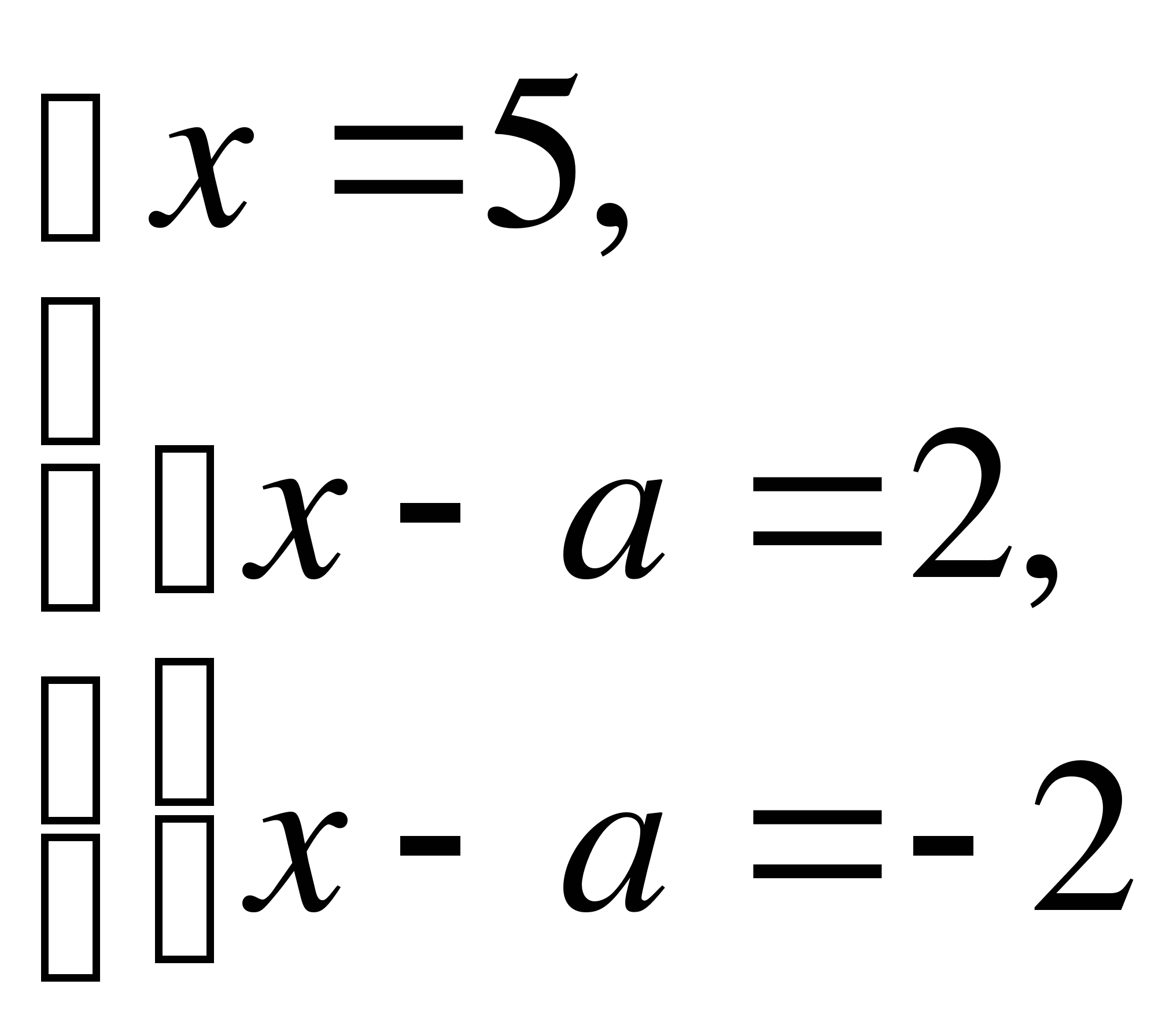
Проверим, имеет ли данное уравнение при найденных значениях единственное решение. При =-3 имеем:

Решим второе уравнение системы:

или
не имеет решений.

Если у=0, то х=5 и (-5; 0) – единственное решение системы. Значит,
не подходит. . Заключение

В ходе проделанной работы был изучен метод инвариантов. Был применён метод инвариантов при решении задач ЕГЭ, содержащих параметр, и олимпиадных задач на раскраску, четность, остатки от деления, обосновано и наглядно показано практическое применение метода.

Список использованной литературы

28 страниц (Word-файл)

Посмотреть все страницы

Фрагмент текста работы

МИНИСТЕРСТВО ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И СВЯЗИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

ХАБАРОВСКИЙ ИНСТИТУТ ИНФОКОММУНИКАЦИИ

(ФИЛИАЛ) ГОУ ВПО СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ

КУРСОВАЯ РАБОТА

по математическим основам цифровой обработки

сигналов

Тема: Расчет рекурсивного цифрового фильтра

Специальность 210405

Радиосвязь, радиовещание и телевидение

Вариант № 30

Выполнил

Руководитель проекта

Зав. Отделением

Хабаровск

	Техническое задание	3
	Исходные данные на вариант № 30	4
	Введение	5
1	Графическое представление задачи	6
1.1	Методы проектирования рекурсивных цифровых фильтров	7
1.2	Методы численного интегрирования	8
1.3	Метод инвариантности импульсной характеристики	10
1.4	Метод билинейного преобразования	12
1.5	Обобщенное биноминальное преобразование	13
2.	Расчет передаточной функции аналогового фильра и преобразование ее в передаточную функцию цифрового фильтра	14
3.	Структурная схема цифрового фильтра	22
4.	Методы реализации цифрового фильтра	23
4.1	Аппаратный метод	23
4.2	Программный метод	24
4.3	Аппаратно-программный метод	25
	Заключение	27
	Список используемой литературы	28

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

По исходным данным необходимо выполнить расчет рекурсивного цифрового фильтра.

Считаются заданными следующие параметры:

1 Вид фильтра: ФНЧ, ФВЧ.

2 Тип фильтра: Баттерворта (Б) или Чебышева (Ч).

3 Частота дискретизации fд.

4 Границы полос пропускания (ПП) :

Верхняя граница полосы пропускания fп для ФНЧ;

Нижняя граница полосы пропускания fп для ФВЧ;

5 Границы полос задерживания (ПЗ);

Нижняя граница ПЗ fз для ФНЧ;

Верхняя граница ПЗ fз для ФВЧ.

6 Допустимая неравномерность амплитудно-частотной характеристики в ПП ∆A max, дБ.

7 Минимально допустимое ослабление в ПЗ А min, дБ.

ИСХОДНЫЕ ДАННЫЕ НА ВАРИАНТ № 30

Вид фильтра ФНЧ

Тип фильтра Баттерворта

Частота дискретизации fд = 16 кГц

Границы полос пропускания fп = 1.7 кГц

Границы полос задерживания fз = 3.8 кГц

Допустимая неравномерность ПП ∆A max = 1.35 дБ

Допустимое ослабление ПЗ А min = 25 дБ.

Преподаватель_____________ Студент___ ____________

“__27__” _______мая_______ 2011 г.

ВВЕДЕНИЕ

Высококачественные частотные нерекурсивные цифровые фильтры (НЦФ) имеют, как правило, большую ширину окна (многочленный оператор фильтра). Чем меньше допустимая ширина переходной зоны частотной характеристики фильтра между полосами пропускания и подавления, тем больше окно фильтра. Альтернативное решение - применение рекурсивных цифровых фильтров (РЦФ), для которых количество коэффициентов фильтра может быть сокращено на несколько порядков по сравнению с НЦФ.

Рекурсивные фильтры имеют определенную "память" по значениям предыдущих отсчетов, которая, в пределе, может быть бесконечной. С учетом этого фактора рекурсивные фильтры получили название фильтров с бесконечной импульсной характеристикой (БИХ-фильтров), в отличие от нерекурсивных фильтров, всегда имеющих конечную импульсную характеристику (КИХ-фильтры). Реакция рекурсивного фильтра на сигнал с учетом "памяти" исключает возможность создания фильтров с четным импульсным откликом, и частотные характеристики рекурсивных фильтров всегда являются комплексными. Проектирование рекурсивных частотных фильтров с заданными частотными характеристиками осуществляется с использованием z-преобразований.

1. Графическое представление задачи

Отобразим графически требования к АЧХ фильтра нижних частот, для этого потребуется вычислить:

Рисунок 1 – АЧХ фильтра Баттерворта и АЧХ фильтра

Баттерворта в Дб.

1.1. Методы проектирования рекурсивных цифровых фильтров

Передаточная функция цифровых БИХ-фильтров задаются соотношением , которая подобна передаточной функции АФ при замене переменной z на s. Следовательно, одним из подходов к проектированию цифровых БИХ-фильтров является преобразование передаточной функции АФ в передаточную функцию ЦФ. Чтобы ЦФ обладали требуемыми свойствами как их АФ, требуется выполнения двух условий:

1. Мнимая ось s-плоскости () отображалась в единичную окружность в z-плоскости (). Это условие необходимо для сохранения частотных характеристик АФ.

2. Левая половина s-плоскости () отображалась в z-плоскости внутри единичного круга (). Это условие необходимо для сохранения свойств устойчивости АФ.

1.2. Метод численного интегрирования

Дифференциальное уравнение, описывающее АФ заменяется на разностное уравнение ЦФ, путем аппроксимации производной некоторыми конечными разностями. Эта операция приводит к замене комплексной переменной s в передаточной функции АФ на комплексную переменную z в передаточной функции ЦФ.

Различные методы численного интегрирования дадут различные функции перехода и, следовательно, различные результирующие ЦФ. Рассмотрим метод Эйлера, аппроксимирующий производную по времени непрерывной функции конечной разностью вида

, где T – интервал дискретизации, а y(n)=y(nT). В операторной форме уравнение дает

.

Покажем, что данный метод удовлетворяет двум выше указанным условиям:

1. или из этого следует что при .

Второй метод дискретизации аналоговых фильтров называется методом инвариантного преобразования импульсной характеристики. Отличительной особенностью этого метода является то, что в качестве импульсной характеристики рассчитываемого цифрового фильтра используется дискретизованная импульсная характеристика соответствующего аналогового фильтра. В результате частотная характеристика цифрового фильтра образуется путем наложений частотной характеристики дискретизованного аналогового фильтра.

Для того чтобы продемонстрировать метод дискретизации аналогового фильтра с использованием инвариантного преобразования его импульсной характеристики, разложим передаточную функцию этого фильтра (4.19) на простые дроби:

, (4.45)

причем каждый коэффициент определяет положение -гo полюса. При записи разложения (4.44) предполагалось, что порядок числителя меньше порядка знаменателя и что все полюсы простые. Предположение о том, что , обязательно должно выполняться для дискретизуемого фильтра, поскольку в противном случае наложения в частотной характеристике цифрового фильтра станут недопустимыми. Если же не все полюсы простые, то результаты, которые будут получены в настоящем разделе, следует несколько модифицировать.

Импульсная характеристика аналогового фильтра с передаточной функцией вида (4.44) описывается соотношением

. (4.46)

Дискретизуя ее, получим импульсную характеристику цифрового фильтра

(4.47)

где - период дискретизации. Найдем ее z-преобразование

(4.48)

Изменив порядок суммирования и просуммировав по , получим

(4.49)

Сравним формулы (4.49) и (4.44). Видно, что для простых полюсов переход от к осуществляется с помощью отображения, при котором используется замена

. (4.50)

Если полюсы комплексные, то остатки в (4.44) также будут комплексными. Функция действительная, поэтому должны существовать также комплексно сопряженные полюс и остаток . Просуммируем эти комплексно сопряженные члены в (4.44):

. (4.51)

Положив и , получим

. (4.52)

Использование отображающей замены (4.50) применительно к каждому слагаемому в формуле (4.51) дает

. (4.54)

Из формул (4.52) и (4.54) получаем

(индекс здесь опущен, а числители поделены на ).

Приведем два полезных частных случая этой отображающей замены, соответствующих аналоговым фильтрам с импульсными характеристиками и :

Выше было отмечено, что частотная характеристика цифрового фильтра, рассчитываемого методом инвариантного преобразования импульсной характеристики, образуется путем наложений частотной характеристики дискретизуемого аналогового фильтра. Таким образом, можно записать

, (4.58)

где - угловая частота дискретизации цифрового фильтра.

Фиг. 4.7. Отображение из s-плоскости в г- плоскость для метода инвариантного преобразования импульсной характеристики.

На фиг. 4.7 показало соответствующее инвариантному преобразованию импульсной характеристики отображение из s-плоскости в z-плоскость. Каждая горизонтальная полоса шириной из -плоскости отображается па z-плоскость. Поэтому все смежные полосы из s-плоскости будут при отображении накладываться друг па друга в z-плоскости. Отсюда следует, что для того, чтобы частотные характеристики исходного аналогового фильтра и рассчитываемого методом инвариантного преобразования импульсной характеристики цифрового фильтра соответствовали друг другу, необходимо, чтобы полоса пропускания аналогового фильтра находилась в пределах диапазона . Для выполнения этого условия необходимо до начала преобразования вводить дополнительный фильтр нижних частот, гарантирующий соответствующее ограничение полосы пропускания аналогового фильтра.

Пример инвариантного преобразования импульсной характеристики. Для иллюстрации этого метода дискретизуем аналоговый фильтр с передаточной функцией вида

Непосредственное использование отображающей замены (4.50) дает

Фиг. 4.8. Амплитудная и фазовая характеристики аналогового фильтра.

Частотная характеристика аналогового фильтра определяется соотношением

.

На фиг. 4.8 представлены амплитудная и фазовая характеристики этого фильтра. Характеристики соответствующего цифрового фильтра для разных значений периода дискретизации изображены на фиг. 4.9. Ясно, что при уменьшении (т. е. при увеличении частоты дискретизации ) эффекты наложения могут оказаться пренебрежимо малыми и частотные характеристики аналогового и цифрового фильтров станут похожими друг на друга.

МЕТОД ИНВАРИАНТА ПРИ РЕШЕНИИ МАТЕМАТИЧЕСКИХ ЗАДАЧ

Остонов К.

(Самаркандский государственный университет)

При решении некоторых математических задач применяется совокупность преобразований искомого объекта и требуется, используя данные преобразования, получить из одного состояния объекта другое. С помощью перебора вариантов в многих случаях можно убедиться в правомерности ответа “нельзя”, но доказательство правильности полученного результата будет сложным. Таким математическим методом решения таких задач считается метод инвариант. Прежде всего определим что такое инвариант?

Определение 1. Инвариантом называется нечто, не меняющееся в преобразованиях.

К примеру, инвариантом могут быть число, набор чисел, четность какого – либо числа и другое.

Свойство 1 . Если значение инварианта в двух состояниях объекта различно, то одно из них нельзя получить из другого.

Во многих математических задачах инвариантом считаются четность (нечетность) чисел и остаток от деления.

Здесь прежде всего основывается на определения четного и нечетного числа, абстрактного понятия четности, чисел имеющие “разную четность”, а также на свойство о том, что при прибавлении единицы четность чисел изменяется. Использование принципа четности и нечетности требует применение следующих утверждений:

Утверждение 1. Четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых.

Утверждение 2. Знак произведения нескольких (отличных от 0) чисел определяется четностью количества отрицательных сомножителей.

Задача 1. На листе бумаги написано число 11. Шестнадцать учеников передают листок друг другу, и каждый прибавляет к числу или отнимает от него единицу – как хочет. Может ли в результате получиться число 0?

Решение. Предлагается выполнить данную операцию учащимся (результат каждого хода записывается на доске), отмечается закономерность: после каждого хода характер четности меняется: после первого ученика число становится четным, после второго нечетным; после третьего - четным; после четвертого – нечетным. Тогда после шестнадцатого число будет нечетным. Поэтому нуль в конце получиться не может.

Задача 2. На вешалке висят 20 платков. 17 девочек по очереди подходят к вешалке и либо снимают, либо вешают платок. Может ли после ухода девочек остаться ровно 10 платков?

Решение. После подхода первой девочки количество оставшихся платков либо 19, либо 21 (нечетное количество); после подхода второй девочки – либо 18, либо 20, либо 22 (четное количество); после подхода третьей девочки – либо 17, либо 21, либо 23, либо 19 (нечетное количество). После подхода 17 девочки остается нечетное количество платков. Получается противоречие. Значит, 10 платков остаться не может.

Задача 3. В таблице, где имеются 15 чисел (-1), можно производить следующую операцию: одновременно изменить знак двух (не более, не меньше) чисел в таблице. Можно ли, применяя эту операцию конечное число раз, получить таблицу, состоящую из (+ 1)?

Решение. Ответ: нельзя. Так как число чисел в таблице нечетно, а после каждой операции число чисел (+ 1) в таблице четно. На языке инвариантов это означает: инвариантом таблицы относительно введенной операции является произведение всех чисел в таблице. В начальный момент это произведение равно (- 1), а нам нужно получить таблицу, инвариант которой равен (+ 1).

Задача 4. Имеется набор чисел Данный набор чисел меняется на тройку чисел:
,
,
. Дан набор чисел 2016, 2018, 2019. Можно ли из него получить набор из чисел 2017, 2018, 2019?

Решение. Ответ: нельзя. Так как
и
+
+
равны, а сумма 2016+ 2018+ 2019 и сумма 2017+ 2018+ 2019 различны.

Задача 5. Из цифр 2, 3, 4,… 9 составили два натуральных числа. Каждая цифра использовалась один раз. Могло ли одно из этих чисел оказаться вдвое больше другого?

Решение. Ответ: нет. Пусть и
– полученные числа, S(a ) и S(b ) – суммы их цифр. По признаку делимости числа N и S(N) имеют одинаковые остатки при делении на 3. Поскольку число a + b = 3a делится на 3, то сумма S = S(a ) + S(b ) должна делиться на 3, что неверно, так как S = 2 + 3 + 4 + … + 9 = 44.

Задача 6. Числа 0,1,2,3, …, 9 записаны по кругу. За один ход разрешается прибавить к двум соседним числам одно и то же целое число. Можно ли за несколько ходов получить десять нулей?

Решение. Нельзя. При прибавлении одинаковых целых чисел к любым двум из имеющихся не меняет четность общей суммы всех чисел. Первоначально эта сумма равно 1 + 2 + 3 + … 9 = 45, следовательно, после каждого хода общая сумма полученных чисел должна быть нечетна, а нуль – четное число.

Задача 7. В десяти сосудах содержится 1, 2, 3,…, 10 литров воды. Разрешается перелить из сосуда А в сосуд В столько воды, сколько имеется в В. Можно ли добиться, чтобы после нескольких переливаний в 5 сосудах оказалось 3 литра, а в остальных 6, 7, 8, 9, 10?

Решение. Нельзя. Предложенная операция обладает полуинвариантом: при любом переливании число нечетных сосудов (содержащих нечетное число литров воды) не увеличивается. Количество таких сосудов уменьшается при переливании из нечетного сосуда в нечетный, а в остальных случаях не изменяется. Следовательно, переход 1, 2, … 10 - 3, 3, 3, 3, 3, 6,…,10 невозможен, поскольку увеличивает число нечетных сосудов.

Решения задач головоломок с использованием четности и нечетности чисел отличаются логической безупречностью и абсолютной обоснован-ностью выводов, которые требует знание на простейших свойств арифме-тических операций сложения и вычитания

Здесь действует следующие основные правила четности:

Сумма четных слагаемых - четна.

Если число нечетных слагаемых четно, то и сумма четна.

Если сумма двух чисел - четное число, то и их разность тоже четное число.

Если сумма двух чисел - нечетное число, то и их разность тоже нечетное число.

Если число нечетных слагаемых нечетно, то и сумма нечетна.

Если один из множителей - четное число, то и произведение четно.

Если все множители нечетны, то и произведение нечетно.

Задача 8 . Четно или нечетно число 1+2+3+4+…+2000? Ответ: четно.

Задача 9. Верно ли равенство 1х2+2х3+3х4+…+99х100 = 20002007? Ответ: нет, сумма четных слагаемых всегда четна.

Задача 10 . .Определить на четность числа 3(х+1); х+х; х+х+2005, если х нечетное. Ответ: первое - четное, второе - четное, третье - нечетное.

Задача 11 . Можно ли квадрат размером 25х25 разрезать на прямоугольники 1х2? Ответ: нет, число 625 не делится на2.

Задача 12 . Можно ли соединить 13 городов дорогами, так чтобы из каждого города выходило ровно 5 дорог? Ответ: нет, каждую дорогу считаем дважды, поэтому общее количество дорог должно быть четным. В нашем случае их 13х5 =65.

Задача 13 . Кузнечик прыгает по прямой: первый раз на 1 см, второй раз на 2 см и т.д. Может ли он через 25 прыжков вернуться на прежнее место? Ответ: нет, чтобы вернуться на старое место общее количество сантиметров должно быть четно, а сумма 1+2+3+…+25 нечетна.

Задача 14 . Можно ли организовать шахматный турнир между 15 шахматистами так, чтобы каждый сыграл по 15 партий? Ответ: нет, 15х15 нечетно.

Задача 15 . Может ли произведение суммы трех последовательных натуральных чисел на сумму трех следующих за ними натуральных чисел быть равным 33333? Ответ: нет, произведение должно быть четно, т.к. один из множителей четное число.

В заключении можно сказать, что применение идеи четности и нечетности позволяет учащимся опровержения тех фактов о которых спрашивается, и понять сходную логику с методом доказательства от противного. При самом распространенном ответе «не может» требуется объяснить почему именно этого не может быть. Если он говорит: «Может», то достаточно привести пример такого расклада, распределения или комбинации. Помимо прямых задач на четность и нечетность может включать в себя разбор близких по замыслу задач (на две противоположности), решаемых при помощи анализа отнесения объекта (или варианта) в ту или иную группу.

Литература

Альхова З. Н., Макеева А. В. Внеклассная работа по математике. – Саратов: «Лицей», 2001.

Виленкин Н. Я. Популярная комбинаторика. - М.: Просвещение, 2003.

Козлова Е. Г. Сказки и подсказки (задачи для математического кружка). Издание 2-е, испр. и доп. – М.: МЦНМО, 2004.

4. Медников Л.Е.Четность.-М.:МЦНМО,2009.

5. Бабич О.А. Сценарий внеурочного занятия по математике(в рамках предметной лаборатории).7 класс.«Инвариант»,г.Холмск, 2015.

6. www.strategy48.ru/sites/default/files/fomina1.pdf

Аннотация

В этой статье рассматривается один из методов решения математических задач – метод инварианта, основанной на идеи четности и нечетности, а также специфика их при решении занимательных задач школьного курса математики.

Ключевые слова : инвариант, задача, идея, четность, число, правила, закномерность.

Метод инварианта цикла является частным случаем метода итераций.

Задается некоторое множество величин М, Р М – подмножество результатов. Надо найти точку х  Р. Для этого выделим множества I M и Q M причем такие, что   I  Q  P. Таким образом, наша задача сводится к нахождению точки, которая будет принадлежать пересечению этих множеств. Причем использовать будем только такие преобразования, которые не выходят из I, то есть в нашем случае принадлежность точки множеству I является инвариантом (величиной неизменной).

Пусть x0  I – начальная точка.

Т:I\QI – преобразование инвариантно относительно принадлежности точки множеству I.

Иллюстрация к вышесказанному:

Под действием преобразования Т точка х0 переходит в некоторую точку х1, принадлежащую множеству I. Точка х1, в свою очередь, переходит в точку х2, также принадлежащую I. Этот процесс продолжается пока некоторая точка хN не перейдет в точку принадлежащую некоторому множеству Q, которое выбрано так чтобы его пересечение с I содержалось в P. Полученная точка с одной стороны принадлежит Q, а с другой принадлежит I, в силу инвариантности преобразования Т относительно I.

Схема программы:

while not q(x) do

{x  IQ  P}

Напишем программу иллюстрирующую вышеописанный метод, которая будет обеспечивать возведенее числа в целую положительную степень.

Type _Real = single;

function power (x: _Real; n: _Unsign ): Real;

{х - основание, n – показатель. Подпрограмма обеспечивает возведение в степень }

while n > 0 do {z*x n - инвариант}

if odd(n) then {проверка нечетности}

dec(n); {n:=n-1}

n:= n chr 1; {n:= n div 2}

Докажем, что данная программа завершится за конечное число шагов. Подпрограмма завершает свою работу когда z = x n , т.е. пердназначена для возведения х в n – ую степень. Число повторений равно количество “0” + 2*количество “1” –1 в двоичной записи числа n <= 2*количество значащих цифр – 1 в двоичной записи = 2*]log 2 n[ - 1. При этом данная программа будет очень эффективна.

Метод инвариантной функции.

Метод инвариантной функции является частным случаем метода инварианта цикла.

В данном случае х = х0 и необходимо вычислить f(x0). При этом

I = {множество x | f(x) = f(x0)}

P = {множество x | f(x) вычисляется легко}.

Построим преобразование Т – инвариантное относительно I, а в качестве условия окончания примем само значение P (Q = P).

Схема программы:

x:= x0; {x  I}

while not p(x) do

begin {x  I\P}

x:= T(x); {x  I}

end; {x  P  I}

Для доказательства правильности достаточно доказать, что цикл выполнится за конечное число шагов.

Напишем программу иллюстрирующую данный метод.

Пусть x = (a, b), а f(x) = Н.О.Д.(a, b). Необходимо вычислить Н.О.Д.(a, b).

В данной программе будет использоваться тот факт, что делитель двух чисел

будет являться делителем их разности.

a:= a0; b:= b0; {>=0}

while (a>0) and (b>0) do

if a>b then a:= a - b

else b:= b – a;

result:= a+b; { условием выхода из цикла является равенство 0 либо a, либо b, поэтому сумма этих чисел будет нам давать то из чисел которое не равно 0 }