Методы их вычисления

Определение . Выражение

называется определителем четвертого порядка. Этот определитель можно записать в виде:

где - минор элемента, стоящего на пересечении i-ой строки и j-го столбца, -алгебраическое дополнение этого элемента.

Формулу (6) можно записать с помощью значка суммирования :

, (7)

где i=1,2,3,4.

Формула (7) называется разложением определителя по элементам

i-ой строки. Можно записать и разложение определителя по элементам j-го столбца:

(8)

где j=1,2,3,4.

Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов строки или столбца определителя в нуль с помощью свойств определителей.

Пример 11. Вычислить определитель

.

Решение . Прибавим элементы первой строки к элементам второй строки:

.

Элементы первой строки умножим на (-2) и прибавим к элементам третьей строки:

.

Элементы первой строки умножим на (-1) и прибавим к элементам четвертой строки:

.

Разложим полученный определитель по элементам первого столбца

Переставим первые две строки, при этом знак определителя изменится на противоположный, одновременно вынесем общий множитель 3 элементов третьего столбца за знак определителя:

.

Умножим элементы первой строки на (-2) и прибавим к элементам второй строки:

.

Полученный определитель разложим по элементам второй строки

Пример 12. Вычислить определитель .

Решение . Поменяем местами первую и вторую строки, при этом по свойству 2 знак определителя изменится на противоположный:

.

Сначала элементы первой строки умножим на (-2) и прибавим к элементам второй и четвертой строк, а затем элементы первой строки умножим на (-3) и прибавим к элементам третьей строки, получим:

.

Элементы второй строки прибавим к элементам четвертой строки:

.

Элементы третьей строки умножим на (-1) и прибавим к элементам четвертой строки:

.

Получим определитель треугольного вида, значение которого равно произведению элементов главной диагонали .

Пример 13 . Вычислить определитель

.

Решение. Разложим определитель по элементам третьей строки

Полученные определители третьего порядка вычислим по правилу треугольника

Задания для самостоятельного решения.

1.Вычислить определители:

2. Решить уравнения:

3. Решить неравенства:

4. Вычислить определители:

Ответы: 1. а)7; б)26; в)0; г)0; д)30. 2 . а)5; б)2; в)2;

г) 3 . а) б) в) г)[-1;7]. 4 . а)-24; б)-40; в)-9; г)57; д)-5; е)1; ж)1; з)55; и)30; к)48; л)0; м)-1004; н)150.

Матрицы

Основные понятия

Определение . Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины и n столбцов одинаковой длины, которая записывается в виде

(9)

или, сокращенно, , где , (т.е. ) – номер строки, (т.е. ) – номер столбца, числа называются элементами матрицы. Матрицу называют матрицей размера и пишут . Например. , .

Определение . Две матрицы и равны между собой, если их размеры совпадают, а их соответствующие элементы равны, т.е. , если , где .

Например. Так как размеры матриц совпадают и соответствующие элементы равны, поэтому матрицы и равны, т.е.

Определение . Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера называют матрицей n-го порядка.

Например. т.е. дана матрица второго порядка.

Определение . Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называются диагональной.

Матрица - диагональная.

Определение . Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой .

или .

Определение . Квадратная матрица называется треугольной, если все элементы, расположенные над главной диагональю (или под главной диагональю), равны нулю.

или - треугольные матрицы.

Важной характеристикой квадратной матрицы порядка n является ее определитель (или детерминант), который обозначается или . .

Определение. Квадратная матрица, у которой определитель отличен от нуля, т.е. , называется невырожденной. В противном случае матрица называется вырожденной.

Например,

Матрица А – вырожденная.

Матрица В – невырожденная.

Определение . Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О.

В матричном исчисление матрицы О и Е играют роль чисел 0 и 1 в арифметике.

Определение . Матрица, содержащая одну строку, называется матрицей-строкой

Матрица размера , состоящая из одного числа, отождествляется с этим числом, т.е. есть 3.

Определение . Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается .

Если , то , если , то .

Транспонированная матрица обладает следующим свойством: .

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 - нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи , то решайте их .»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

С каждой квадратной матрицей связывают число . Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A , ΔA.

Число строк (столбцов) определителя называется его порядком .

Определитель первого порядка матрицы равен элементу a 11: |A|=a 11

Не путать определитель первого порядка с модулем.

Определитель второго порядка обозначается символом

и равен |A|=a 11 a 22 -a 12 a 21

Определитель 3-го порядка обозначается символом

Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса )

Правило Саррюса.

Правило треугольника.

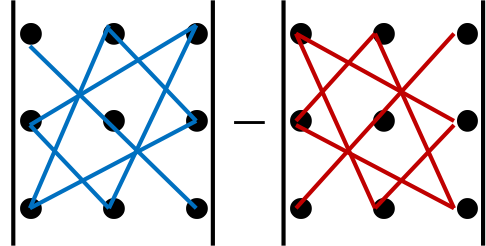
Посмотрим на примере, как используются эти правила.

ПРИМЕР:

Правило Саррюса

Допишем к определителю два первых столбца.

Правило треугольника

Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.

Алгебраическим дополнением (А ij ) элемента а ij определителя матрицы А называется число, равное произведению (-1) i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.

ПРИМЕР:

Вычислить алгебраическое дополнение А 21 элемента а 21 .

РЕШЕНИЕ:

По определению алгебраического дополнения

Вычисление определителя произвольного порядка. Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.

, разложение определителя 4-го порядка по первой строке выглядит следующим образом:

Инструкция

Для вычисления детерминанта (Det A) матрицы размерностью 5х5 проведите элементов по первой строке. Для этого возьмите первый элемент данной строки и вычеркните из матрицы строку и столбец, на пересечении которых он находится. Запишите формулу произведения первого и определителя полученной матрицы 4 порядка: a11*detM1 – это будет первое слагаемое для нахождения Det A. В оставшейся четырехразрядной матрице М1 вам будет позже так же найти определитель (дополнительный минор).

Аналогичным образом, последовательно вычеркивайте столбец и строку, содержащие 2, 3, 4 и 5 элемент первой строки начальной матрицы, и находите для каждого из них соответствующую матрицу 4х4. Запишите произведения этих элементов на дополнительные миноры: a12*detM2, a13*detM3, a14*detM4, a15*detM5.

Найдите определители полученных матриц 4 порядка. Для этого проведите тем же методом понижение размерности. Первый элемент b11 матрицы M1 умножьте на определитель оставшейся матрицы 3х3 (C1). Детерминант же трехмерной матрицы можно легко по формуле: detC1 = c11* c22*c33 + c13* c21*c32 + c12* c23*c31 - c21* c12*c33 - c13* c22*c31 - c11* c32*c23, где cij – элементы полученной матрицы C1.

Далее рассмотрите аналогично второй элемент b12 матрицы М1 и вычислите его с соответствующим дополнительным минором detC2 полученной трехмерной матрицы. Таким же образом найдите произведения для 3 и 4 элемента первой матрицы 4 порядка. После чего определите искомый дополнительный минор матрицы detМ1. Для этого, согласно формуле разложения по строке, : detМ1 = b11*detC1 - b12*detC2 + b13*detC3 - b14*detC4. Вы получили первое слагаемое, необходимое для нахождения Det A.

Вычислите остальные слагаемые определителя матрицы пятого порядка, аналогичным образом понижая размерность каждой матрицы 4 порядка. Окончательная так: Det A = a11*detM1 - a12*detM2 + a13*detM3 - a14*detM4 + a15*detM5.

Инструкция

Самая простая и краткая формулировка этой операции такова: матрицы перемножаются по алгоритму "строка на столбец".

Теперь подробнее об этом правиле, а также о возможных ограничениях и особенностях.

Умножение на единичную матриц переводит исходную матрицы саму в себя (эквивалентно умножению чисел, где один из элементов 1). Аналогично, умножение на нулевую матрицу даёт нулевую матрицу.

Главное условие, накладываемое на участвующие в операции матрицы вытекает из способа выполнения : строк в первой матрице должно быть столько же, сколько столбцов во второй. Нетрудно догадаться, что в противном просто не на что.

Также стоит отметить ещё один важный момент: у умножения матриц нет коммутативности (или "перестановочности"), иначе говоря, А умножить на B не равняется B умножить на А. Запомните это и не путайте с правилом для умножения чисел.

Теперь, собственно сам процесс умножения.

Пусть мы умножаем матрицу А на матрицу B справа.

Берём первую строчку матрицы А и ее i-ый элемент умножаем на i-ый элемент первого столцба матрицы B. Все полученные складываем и записываем на место а11 в итоговую матрицу.

Затем также поступаем с первой строкой матрицы А и 3-им, 4-ым и т.д. столбцами матрицы Б, заполнив, таким образом, первую строчку итоговой матрицы.

Теперь переходим ко второй строке и снова перемножаем её последовательно на все столбцы, начиная с первого. Записываем результат во вторую строку итоговой матрицы.

Затем к 3-ей, 4-ой и т.д.

Повторяем , пока не перемножим все строки в матрице А со всеми столбцами матрицы В.

Матрицы - это эффективный способ представления числовой информации. Решение любой системы линейных уравнений можно записать в виде матрицы (прямоугольника, составленного из чисел). Умение перемножать матрицы - один из самых важных навыков, которым обучают на курсе "Линейной алгебры" в высших учебных заведениях.

Вам понадобится

• Калькулятор

Инструкция

Для проверки этого условия проще всего воспользоваться следующим алгоритмом - запишите размерность первой матрицы как (a*b). Дальше размерность второй - (c*d). Если b=c - матрицы соразмерны, их можно перемножать.

Дальше произведите само перемножение. Помните - при перемножении двух матриц получается матрица. То есть, задача перемножения сводится к задаче нахождения новой, с размерностью (a*d). На СИ задачи перемножения матрицы выглядит следующим образом:
void matrixmult(int m1[n], int m1_row, int m1_col, int m2[n], int m2_row, int m2_col, int m3[n], int m3_row, int m3_col)
{ for (int i = 0; i < m3_row; i++)
for (int j = 0; j < m3_col; j++)
m3[i][j]=0;
for (int k = 0; k < m2_col; k++)
for (int i = 0; i < m1_row; i++)
for (int j = 0; j < m1_col; j++)
m3[i][k] += m1[i][j] * m2[j][k];
}

Проще говоря, новой матрицы - это сумма произведений элементов строки первой матрицы на элементы столбца второй матрицы. Если вы элемент третьей матрицы с номером (1;2), то вы должны просто умножить первую строку первой матрицы на второй столбец второй. Для этого считаете начальную сумму равной нулю. Дальше умножаете первый элемент первой строки на первый элемент второго столбца, значение добавляете в сумму. Делаете так: умножаете i-тый элемент первой строки на i-тый элемент второго столбца и добавляете результаты к сумме, пока не кончится строка. Итоговая сумма и будет искомым элементом.

После того, как вы нашли все элементы третьей матрицы, записываете ее. Вы нашли произведение матриц.

Источники:

• Главный математический портал России в 2019
• как находить произведение матриц в 2019

Определитель (детерминант) матрицы - одно из важнейших понятий линейной алгебры. Определитель матрицы представляет собой многочлен от элементов квадратной матрицы. Чтобы вычислить определитель четвертого порядка, нужно общим правилом вычисления определителя.

Вам понадобится

Инструкция

Квадратная матрица четвертого представляет из себя из четырех строк и четырех столбцов. Ее определитель считается по общей рекурсивной формуле, приведенной на рисунке. M с индексами является дополнительным минором этой матрицы. Минор квадратной матрицы порядка n M с индексом 1 вверху и индексами от 1 до n внизу, - это определитель матрицы, который получается из исходной вычеркиванием первой строки и j1...jn столбцов (j1...j4 столбцов в случае квадратной матрицы четвертого порядка).

Из этой следует, что в результате для определителя квадратной матрицы четвертого порядка представит из себя сумму из четырех слагаемых. Каждое слагаемой будет являться произведением ((-1)^(1+j))aij, то есть одного из членов перовой строки матрицы, взятого с положительным или знаком, на квадратную третьего порядка (минор квадратной матрицы).

Получившиеся миноры, которые представляют из себя матрицы третьего порядка, можно уже по известной частной формуле, без использования новых миноров. Определители квадратной матрицы третьего порядка можно рассчитать по так называемому «правилу треугольника». Формулу для расчета определителя в этом случае выводить не нужно, а можно запомнить ее геометрическую схему. Эта изображена на приведенном рисунке. В результате |А| = a11*a22*a33+a12*a23*a31+a13*a21*a32-a11*a23*a32-a12*a21*a33-a13*a22*a31.
Следовательно, миноры вычислены и определитель квадратной матрицы четвертого порядка может быть посчитан.

Источники:

• как рассчитать определитель

Вам понадобится

• - программа Microsoft Office Excel.

Инструкция

Запустите программу Microsoft Office Excel. В меню ввода данных впишите данную вам матрицу для последующего вычисления ее определителя. Выделите одну из незанятых ячеек таблицы, после чего введите следующую формулу: “=МОПРЕД(ak:fg)”. В данном случае ak будет означать координаты, соответствующие левому верхнему углу заданной матрицы, а fg – нижнему правому. Для получения определителя нажмите клавишу Enter. Нужное значение будет отображено в выбранной вами пустой ячейке.

Используйте функционал Excel для вычисления и других значений. В случае если вы не умеете использовать формулы в Microsoft Office Excel, скачайте специальную тематическую литературу, и после прочтения вам будет достаточно легко сориентироваться по данной программе.

Внимательно изучите наименования значений формул в данном программном обеспечении, поскольку при неправильном их вводе у вас могут испортиться сразу все результаты, в особенности это касается тех, кто выполняет сразу несколько одинаковых вычислений по одной одновременно.

Время от времени выполняйте проверку полученных в Microsoft Office Excel результатов вычисления. Это связано с тем, что в системе могли произойти какие-либо изменения со временем, в частности это относится к тем, кто выполняет работу по шаблона. Всегда нелишним будет лишний раз сверить результаты сразу нескольких текущих вычислений.

Также при работе с формулами будьте крайне осторожны и не допускайте появления в вашем компьютере вирусов. Даже в случае если операции с формулами в Microsoft Office Excel понадобится вам единоразово, изучите функционал данной программы в большей степени, поскольку эти навыки помогут вам в дальнейшем лучше понимать автоматизацию учета и применять Excel для выполнения определенных заданий.

Определитель – одно из понятий матричной алгебры. Это квадратная матрица, состоящая из четырех элементов, а чтобы вычислить определитель второго порядка , нужно воспользоваться формулой разложения по первой строке.

Инструкция

Определитель квадратной – это , которое используется в различных расчетах. Он незаменим при нахождении обратной матрицы, миноров, алгебраических дополнений, операции деления , но чаще всего необходимость перехода к определителю возникает при решении систем линейных уравнений.

Матрица второго порядка представляет собой совокупность четырех элементов, расположенных на двух строках и столбцах. Эти числа соответствуют коэффициентам системы уравнений неизвестными, которые применяются при рассмотрении множества прикладных задач, например, экономических.

Переход к компактным матричным вычислениям помогает быстро две вещи: во-первых, имеет ли эта решение, во-вторых, найти его. Достаточным условием решения является

Второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ; detA (детерминант).

.

Пример:
.

Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу

Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.

В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.

Пример:

Разложение определителя по элементам некоторой строки (столбца).

Минором М ij элемента а ij квадратной матрицы А называется определитель, составленный из элементов матрицы А , оставшихся после вычеркивания i- ой строки и j -го столбца.

Например, минором к элементу а 21 матрицы третьего порядка
будет определитель
.

Будем говорить, что элемент а ij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) - четное число, нечетное место, если i+j - нечетное число.

Алгебраическим дополнением А ij элемента а ij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).

Пример:

а 23 = 4;

- алгебраическое дополнение элемента а 22 = 1.

Теорема Лапласа . Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

Проиллюстрируем на примере определителя третьего порядка. Вычислить определитель третьего порядка разложением по первой строке можно следующим образом

Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.

Пример :

Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы n -го порядка, сводя его к вычислению n определителей (n-1 )-го порядка

Замечание. Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.

Пример . Вычислить определитель четвертого порядка.

Разложим определитель по элементам третьей строки

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.

5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.