где – оператор Гамильтона – аналог классической функции Гамильтона
в которой и заменены операторами импульса x , y , z и координаты , , :
х → = х, y → = y, z → = z,
| (4.2) |
Уравнение ШредингераЗависящее от времени уравнение Шредингера: где – гамильтониан системы. Разделение переменных. Запишем Ψ(,t) = ψ()θ(t), где ψ является функцией координат, а θ – функция времени. Если не зависит от времени, тогда уравнение ψ = iћψ принимает вид θψ = iћψθ или Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
Следовательно, θ(t) = exp(−iEt/ћ), ψ() = Eψ() и Ψ(,t) = ψ()exp(−iEt/ћ). Уравнение ψ() = Eψ() называют стационарным уравнением Шредингера. Для одномерной системы с массой m в поле с потенциалом U(x) оно принимает вид:
Для трехмерной системы с массой m в поле с потенциалом U(): −(ћ 2 /2m)Δψ() + U()ψ() = Eψ(), где Δ – лапласиан. |
или
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
| ψ() = Eψ(). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
| Ψ(,t) = ψ()exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(,t)|, то она ~ |ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2 . Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
где k = (2mE/ћ 2) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
Частица может находиться в
каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии E n соответствует
волновая функция ψ n (x), которая с учетом
условия нормировки
имеет вид
 |
(4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может
иметь энергию
E < ћ 2 π 2 /(2mL 2).
Состояния частицы ψ n в
одномерном поле бесконечной потенциальной ямы полностью описывается с помощью
одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3 . Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
Допустимые значения полной энергии определяются формулой
| E n = ћω 0 (n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического
осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое
описание частицы переходит в классическое.
4.4 . Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
где радиальная функция R nl (r) и угловая функция Y lm (θ,φ), называемая сферической, удовлетворяют уравнениям
| 2 Y lm (θ,φ) = ћ 2 l (l +1)Y lm (θ,φ) | (4.16) |
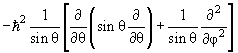 Y lm (θ,φ)
= ћ 2 l
(l
+1)Y lm (θ,φ) |
(4.17) |
Уравнение (4.16) определяет возможные собственные значения
l
и собственные функции Y lm (θ,φ) оператора
квадрата момента 2 .
Уравнение (4.17) определяет собственные значения энергии Е и радиальные
собственные функции R nl (r),
от которых зависит энергия системы (рис. 4.3).
Схема уровней (последовательность и абсолютные значения энергий) зависит от
радиальной функции R nl (r),
которая в свою очередь определяется потенциалом U(r),
в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в
кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r 0 = ћ 2 /m e e 2 ≈
0.529·10 8 cм.
4.5 . Орбитальный момент количества движения
Собственные значения L 2 и L z являются решением уравнений
2 Y lm (θ,φ) = L 2 Y lm (θ,φ) и z Y lm (θ,φ) = L z Y lm (θ,φ).
Они имеют следующие дискретные значения
L 2 =
ћ 2 l(l
+ 1), где l = 0, 1, 2, 3, …,
L z =
ћm,
где m = 0, ± 1,
± 2, ± 3,…,
± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная
волновая функция. В тех случаях, когда l ≠ 0
волновая функция не имеет сферической симметрии. Симметрия волновой функции
определяется симметрией сферических функций Y lm (θ,φ).
Имеет место интересное квантовое явление, когда решение сферически симметричной
задачи (потенциал описывает сферически симметричную систему) приводит к
состояниям, не обладающим сферической симметрией. Таким образом, симметрия
уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого
решения этих уравнений, а лишь во всей совокупности
этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина
орбитального момента количества движения L:
| (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
=
= 6.58·10 -22 √6
МэВ·сек ≈ 2.6·10 - 34
Дж·сек.
Пространственное квантование
. Орбитальный момент количества движения является
векторной величиной. Так как величина орбитального момента количества движения
квантуется, то и направление
по
отношению к выделенному направлению z, например, к
внешнему магнитному полю, также квантуется и принимает дискретные значения
Lz =
ћm,
где m изменяется от +l до –l,
т. е. имеет 2l + 1 значений. Например, при
l = 2 величина m принимает
значения +2, +1, 0, -1, -2 (см. рис. 4.4). Вместе с тем энергия системы не
зависит от m, т. е. от направления вектора
,
что является очевидным следствием сферической симметрии системы.
Состояние частицы, находящейся в сферически симметричном поле, полностью
описывается тремя квантовыми числами: n,
l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер
этой симметрии определяет возможные значения квантовых чисел. Очевидно, что
система, описываемая функцией e im φ , примет прежнее
значение только тогда, когда азимутальный угол φ в результате поворота вокруг
оси z примет прежнее значение φ. Этому условию функция
e im φ удовлетворяет только в случае, когда величина
mφ кратна 2π. Т.е. величина m
должна иметь целые значения. Так как необходимо учитывать вращение в двух
противоположных направлениях и отсутствие вращения, единственно возможными
значениями оказываются m = 0, ±1, ±2, … .
4.6 . Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина и квантовым числом спина s выполняется такое же соотношение, как между величиной значением вектора орбитального момента и орбитальным квантовым числом l:
| 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l,
которое может быть лишь целым числом или нулем, спиновое квантовое число
s (в дальнейшем просто спин) может быть как целым
(включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2,
… , но при этом для каждой элементарной частицы спин может принимать
единственное присущее этому типу частиц значение
. Так, спины π-мезонов и К-мезонов
равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2.
Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина,
спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также
как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина
на
любое фиксированное направление в пространстве (например, на ось
z) может принимать 2s + 1
значение:
s z ћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ,..., ±1/2ћ или 0.
Число s z − это квантовое число проекции спина. Максимальная величина s z совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения s z = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7 . Полный момент количества движения
Полный момент количества движения частицы или системы частиц является векторной суммой орбитального и спинового моментов количества движения.
Квадрат полного момента имеет значение:
2 = ћ 2 j(j + 1).
Квантовое число полного момента j, соответствующее сумме двух векторов и , может принимать ряд дискретных значений, отличающихся на 1:
j = l + s, l + s −1,..., |l − s|
Проекция на выделенную ось J z также принимает дискретные значения:
J z = ћj z ; = -j, -j + 1,..., j − 1, j.
Число значений проекции J z равно 2j + 1. Если для и определены единственные значения проекций на ось z l z и s z , то j z также определена однозначно: j z = l z + s z .
4.8 . Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы. 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| s z | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения s z ћ, где s z = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии → - (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков - отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n (1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
где U 0 ,
а и R – положительные константы (R
– радиус ядра). Во всех случаях сферически симметричные системы можно
описать с помощью набора квантовых чисел n,
l, j,
j z ,
однако, в зависимости от радиального вида потенциала энергетический спектр
состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со
свойствами симметрии гамильтониана системы. Например, в случае, если квантовая
система обладает центральной симметрией U = U(r),
то этой системе соответствует сохранение орбитального момента количества
движения l и одной из его проекций
m. При этом из-за сферической симметрии задачи энергия состояний не будет
зависеть от величины m, т. е. состояния будут
вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными
преобразованиями, в квантовой физике существуют и другие симметрии –
дискретные. Одной из них является зеркальная симметрия волновой функции
относительно инверсии координат (→
-).
Оператору инверсии соответствует квантовое число четность, которое может
принимать два значения +1 и -1 в зависимости от того, сохраняется ли знак
волновой функции при инверсии или меняется на противоположный.
Система тождественных частиц характеризуется еще одной симметрией –
симметрией относительно перестановок тождественных частиц. Эта симметрия
определяется свойствами частиц, образующих систему. Системы частиц с целым
спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым
спином (фермионов) − антисимметричными волновыми функциями.
Стационарные решения уравнения Шредингера.
Приложение A.
Нахождение решения уравнения Шредингера для свободного электрона в виде волнового пакета .
Запишем уравнение Шредингера для свободного электрона
После преобразований уравнение Шредингера принимает вид
(A.2)
Это уравнение решаем с начальным условием
(A.3)
Здесь - волновая функция электрона в начальный момент времени. Ищем решение уравнения (A.2) в виде интеграла Фурье
(A.4)
Подставляем (A.4) в (A.2) и получаем
Решение (A.4) можно теперь записать в следующем виде
(A.6)
Используем начальное условие (A.3), и из (A.6) получаем разложение начальной волновой функции электрона в интеграл Фурье.
(A.7)
К выражению (A.7) применяем обратное преобразование Фурье
(A.8)
Подведем итог проделанным преобразованиям. Итак, если известна волновая функция электрона в начальный момент времени, то после интегрирования (A.8) находим коэффициенты . Затем после подстановки этих коэффициентов в (A.6) и интегрировании, получаем волновую функцию электрона в произвольный момент времени в любой точке пространства.
Для некоторых распределений интегрирование можно провести в явном виде и получить аналитическое выражение для решения уравнения Шредингера. В качестве начальной волновой функции возьмем распределение Гаусса, модулированное плоской монохроматической волной.
Здесь - средний импульс электрона. Выбор начальной волновой функции в таком виде позволят получить решение уравнения Шредингера в виде волнового пакета.
Рассмотрим подробно свойства начальной волновой функции (A.9).
Во-первых , волновая функция нормирована на единицу.
(A.10)
Нормировка (A.10) легко доказывается, если использовать следующий табличный интеграл.
(A.11)
Во-вторых , если волновая функция нормирована на единицу, то квадрат модуля волновой функции является плотностью вероятности, нахождения электрона в данной точке пространства.
Здесь величину будем называть амплитудой волнового пакета в начальный момент времени. Физический смысл амплитуды пакета – это максимальное значение распределения вероятности. На Рис.1 показан график распределения плотности вероятности.
Распределение плотности вероятности в начальный момент времени.
Отметим некоторые особенности графика на Рис.1.
1. Координата – это точка на оси x , в которой распределение вероятности имеет максимальное значение. Поэтому можно сказать, что с наибольшей вероятностью можно обнаружить электрон вблизи точки .
2. Величина определят отклонение от точки , при котором величина распределения уменьшается в e раз по сравнению с максимальным значением.
(A.13)
В этом случае величину называют шириной волнового пакета в начальный момент времени, а величину – полушириной пакета.
3. Вычислим вероятность нахождения электрона в интервале 
.
(A.14)
Таким образом, вероятность обнаружить электрон в области с центром и полушириной равна 0.843. Эта вероятность близка к единице, поэтому обычно, об области с полушириной говорят, как об области, где находится электрон в начальный момент времени.
В-третьих , начальная волновая функция не является собственной функцией оператора импульса . Поэтому электрон в состоянии с волновой функцией не имеет определенного импульса, можно говорить только о среднем импульсе электрона. Вычислим средний импульс электрона.
Поэтому, величина в формуле (A.9) является средним значением импульса электрона. Формула (A.15) легко доказывается, если использовать табличный интеграл (A.11).
Таким образом, свойства начальной волновой функции разобраны. Теперь подставим функцию в интеграл Фурье (A.8) и найдем коэффициенты .
В интеграле (A.16) делаем следующую замену переменной интегрирования.
(A.17)
В результате интеграл (A.16) принимает следующий вид.
(A.18)
В результате получаем следующее выражение для коэффициентов .
(A.18)
Подставляем коэффициенты в формулу (A.6), получаем следующее интегральное выражение для волновой функции.
В интеграле (A.19) делаем следующую замену переменной интегрирования.
(A.20)
В результате интеграл (A.19) принимает следующий вид.
Окончательно получаем формулу для волнового пакета.
(A.22)
Легко видеть, что для начального момента времени формула (A.22) переходит в формулу (A.9) для начальной волновой функции. Найдем плотность вероятности для функции (A.22).
Подставляем волновой пакет (A.22) в формулу (A.23), и в результате получаем следующее выражение.
(A.24)
Здесь центр волнового пакета, или максимум распределения плотности вероятности, движется со скоростью , равной следующей величине.
Полуширина волнового пакета увеличивается со временем, и определятся следующей формулой.
(A.26)
Амплитуда волнового пакета уменьшается со временем, и определятся следующей формулой.
(A.27)
Таким образом, распределение вероятности для волнового пакета можно записать в следующем виде.
(A.28)
На Рис.2. показано распределение вероятности в три последовательных момента времени.
Распределение вероятности в три последовательных момента времени.
Приложение B.
Общие сведения о решении уравнения Шредингера .
Введение.
Движение квантовой частицы в общем случае описывается уравнением Шредингера:
Здесь i – мнимая единица, h =1.0546´10 -34 (Дж×с) - постоянная Планка. Оператор Ĥ называется оператором Гамильтона. Вид оператора Гамильтона зависит от типа взаимодействия электрона с внешними полями.
Если не учитывать спиновые свойства электрона, например, не рассматривать движение электрона в магнитном поле, то оператор Гамильтона можно представить в виде.
(B.2)
Здесь – оператор кинетической энергии:
, (B.3)
где m =9.1094´10 -31 (кг) – масса электрона. Потенциальная энергия описывает взаимодействие электрона с внешним электрическим полем.
В данной лабораторной работе будет рассматриваться одномерное движение электрона вдоль оси x . Уравнение Шредингера в этом случае принимает следующий вид:
. (B.4)
Уравнение (B.4) с математической точки зрения является дифференциальным уравнение в частных производных для неизвестной волновой функции Y =Y (x,t). Известно, что такое уравнение имеет определенное решение, если заданы соответствующие начальные и граничные условия. Начальные и граничные условия выбираются исходя из конкретной физической задачи.
Пусть, например, электрон движется слева направо с некоторым средним импульсом p 0 . Кроме того, в начальный момент времени t=0, электрон локализован в некоторой области пространства x m -d < x < x m +d. Здесь x m – центр области локализации электрона, а d – эффективная полуширина этой области.
В этом случае начальное условие будет выглядеть следующим образом:
. (B.5)
Здесь Y 0 (x) – волновая функция в начальный момент времени. Волновая функция это комплексная функция, поэтому графически удобно представлять не саму волновую функцию, а плотность вероятности.
Плотность вероятности, нахождения электрона в данном месте в данный момент времени выражается через волновую функцию следующим образом:
Заметим, что вероятности должна быть нормирована на единицу. Отсюда получаем условие нормировки волновой функции:
. (B.7)
Распределение плотности вероятности в начальный момент времени
, (B.8)
можно изобразить графически. На Рис.3. показано возможное расположение электрона в начальный момент времени.
Расположение электрона в момент t=0.
Из этого рисунка видно, что с наибольшей вероятностью электрон находится в точке x m . Буквой A будем обозначать амплитуду (максимальное значение) распределения вероятности. Из этого рисунка так же видно, как определяется ширина 2d или полуширина d распределения. Если распределение имеет экспоненциальный или гауссов характер, то ширину распределения определяют на уровне в e раз меньшем, чем максимальное значение.
На Рис.3. показан вектор среднего импульса электрона. Это означает, что электрон движется справа налево, и распределение вероятности так же будет перемещаться справа налево. На Рис.2. показано распределение вероятности в три последовательных момента времени. На Рис.2. видно, что максимум распределения x m (t) перемещается слева направо.
На Рис.2. можно заметить, что движение электрона справа налево сопровождается деформацией распределения плотности вероятности. Амплитуда A (t) уменьшается, а полуширина d(t) растет. Все указанные детали движения электрона можно получить, если решить уравнение Шредингера (B4) с начальным условием (B.5).
Резюме . В зависимости от постановки физической задачи может меняться вид уравнения Шредингера. При исследовании тех или иных физических явлений, описываемых уравнением Шредингера, выбираются нужные начальные и граничные условия для нахождения решения уравнения Шредингера.
Стационарные решения уравнения Шредингера.
Если электрон движется в постоянном по времени внешнем поле, то его потенциальная энергия не будет зависеть от времени. В этом случае одним из возможных решений уравнения Шредингера (B.4) является решение с разделяющимися переменными по времени t и по координате x.
Применяем известный в математике прием решения дифференциальных уравнений. Ищем решение уравнения (B.4) в виде:
. (B.9)
Подставляем (B.9) в уравнение (B.4) и получаем следующие соотношения:
. (B.10)
Здесь E – константа, которой в квантовой механике придается смысл полной энергии электрона. Соотношения (B.10) эквивалентны следующим двум дифференциальным уравнениям:
. (B.11)
Первое уравнение в системе (B.11) имеет следующее общее решение:
Здесь C – произвольная константа. Подставляем (B.12) в выражение (B.9) и получаем решение уравнения Шредингера (B.4) в виде:
, (B.13)
где функция y (x) удовлетворяет уравнению.
(B.14)
Константа C содержится в функции y (x).
Решение уравнения Шредингера (B.4) в виде выражения (B.13), называется стационарным решением уравнения Шредингера . Уравнение (B.14) называют стационарным уравнение Шредингера . Функцию y (x) называют волновой функцией , независящей от времени.
Состояние электрона, которое описывается волной функцией (B.13), называется стационарным состоянием . В квантовой механике утверждается, что в стационарном состоянии электрон обладает определенной энергией E .
Полученные результаты можно обобщить на уравнение Шредингера (B.1) для трехмерного движения электрона. Если оператор Гамильтона Ĥ не зависит явно от времени, то одним из возможных решений уравнения Шредингера (B.1) является стационарное решение следующего вида:
, (B.15)
где волновая функция удовлетворяет стационарному уравнению Шредингера.
(B.16)
Заметим, что уравнения (B.14) и (B.16) в квантовой механике имеют еще оно название. Эти уравнения являются уравнениями на собственные функции и собственные значения оператора Гамильтона. Другими словами, решая уравнение (B.16) находят энергии E (собственные значения оператора Гамильтона) и соответствующие им волновые функции (собственные функции оператора Гамильтона).
Резюме . Стационарные решения уравнения Шредингера являются некоторым классом решений из огромного множества других решений уравнения Шредингера. Стационарные решения существуют, если оператор Гамильтона не зависит явно от времени. В стационарном состоянии электрон имеет определенную энергию. Для нахождения возможных значений энергии надо решить стационарное уравнение Шредингера.
Волновой пакет.
Легко видеть, что стационарные решения уравнения Шредингера не описывают движение локализованного электрона, как показано на Рис.1 и Рис.2. Действительно, если взять стационарное решение (B.13) и найти распределение вероятности, то получится функция независящая от времени.
(B.17)
В этом нет ничего удивительного, стационарное решение (B.13) является одним из возможных решений дифференциального уравнения в частных производных (B.4).
Но вот что интересно, в силу линейности уравнения Шредингера (B.4) относительно волновой функции Y (x,t), для решений этого уравнения выполняется принцип суперпозиции. Для стационарных состояний этот принцип утверждает следующее. Любая линейная комбинация стационарных решений (с разными энергиями E ) уравнения Шредингера (B.4) то же является решением уравнения Шредингера (B.4).
Чтобы дать математическое выражение для принципа суперпозиции, нужно сказать несколько слов об энергетическом спектре электрона. Если решение стационарного уравнения Шредингера (B.14) имеет дискретный спектр, то это означает, что уравнение (B.14) можно записать в следующем виде:
(B.18)
где индекс n пробегает, вообще говоря, бесконечный ряд значений n=0,1,2,¼ . В этом случае решение уравнения Шредингера (B.4) можно представить в виде суммы стационарных решений.
(B.19)
В квантовой механике доказывается, что собственные функции y n (x) дискретного спектра можно сделать ортонормированной системой функций. Это означает, что выполняется следующее условие нормировки.
(B.20)
Здесь d n m – символ Кронекера.
y n (x) ортонормированная, то коэффициенты C n в сумме (B.19) имеют простой физический смысл. Квадрат модуля от коэффициента C n равен вероятности того, что электрон в состоянии с волновой функцией (B.19) имеет энергию E n .
Самое главное в этом утверждении, что электрон в состоянии с волновой функцией (B.19) не имеет определенной энергии. При измерении энергии, у этого электрона может быть получена любая энергия из набора с вероятностью (B.21).
Поэтому говорят, что электрон может обладать той или иной энергией с вероятностью, определяемой формулой (B.21).
Электрон, который находится в стационарном состоянии и имеет определенную энергию, будем называть монохроматическим электроном . Электрон, который не находится в стационарном состоянии, и поэтому не имеет определенной энергии, будем называть немонохроматическим электроном .
Если решение стационарного уравнения Шредингера (B.14) имеет непрерывный спектр, то это означает, что уравнение (B.14) можно записать в следующем виде:
, (B.22)
где энергия E принимает значения на некотором непрерывном интервале [E min , E max ]. В этом случае решение уравнения Шредингера (B.4) можно представить в виде интеграла стационарных решений.
(B.23)
Собственные функции непрерывного спектра y E (x) в квантовой механике принято нормировать на d-функцию:
, (B.24)
Определение d-функции содержится в следующих интегральных соотношениях:
Чтобы наглядно представить поведение d-функции, приводят следующее описание этой функции:
Так вот, если система функций y E (x) нормирована на d-функцию, то квадрат модуля от коэффициента C (E ) в интеграле (B.23) равен плотности вероятности того, что электрон в состоянии с волновой функцией (B.19) имеет энергию E .
Волновая функция Y(x,t) представленная в виде суммы (B.19) или в виде интеграла (B.23) от стационарных решений уравнения Шредингера, называется волновым пакетом .
Таким образом, состояние не монохроматического электрона описывается волновым пакетом. Можно сказать еще так, в состояние немонохроматического электрона дают вклад состояния монохроматического электрона со своими весовыми множителями.
На Рис.1. и Рис.2. изображены волновые пакеты электрона в разные моменты времени.
Резюме . Состояние немонохроматического электрона описывается волновым пакетом. Немонохроматический электрон не обладает определенной энергией. Волновой пакет можно представить суммой или интегралом волновых функций стационарных состояний со своими энергиями. Вероятность того, что немонохроматический электрон имеет ту или иную энергию из этого набора энергий, определятся вкладом соответствующих стационарных состояний в волновой пакет.
Свободное движение. Общее решение уравнения Шредингера.
В зависимости от поля, с которым взаимодействует электрон, решение стационарного уравнения Шредингера (B.14) может иметь разный вид. В данной лабораторной работе рассматривается свободное движение. Поэтому в уравнении (B.14) положим потенциальную энергию равной нулю. В результате получим следующее уравнение:
, (B.26)
общее решение этого уравнения имеет следующий вид:
. (B.27)
Здесь C 1 и С 2 - две произвольные константы, k имеет смысл волнового числа.
Теперь с помощью выражения (B.23) запишем общее решение уравнения Шредингера для свободного движения. Подставляем функцию (B.27) в интеграл (B.23). При этом учитываем, что пределы интегрирования по энергии E для свободного движения выбираются от нуля до бесконечности. В результате получаем следующее выражение:
В этом интеграле удобно перейти от интегрирования по энергии E к интегрированию по волновому числу k . Будем считать, что волновое число может принимать как положительные, так и отрицательные значения. Для удобства введем частоту w, связанную с энергией E , следующим соотношением:
Преобразуя интеграл (B.28), получаем следующее выражение для волнового пакета:
. (B.30)
Интеграл (B.30) дает общее решение уравнения Шредингера (B.4) для свободного движения. Коэффициенты C (k) находятся из начальных условий.
Возьмем начальное условие (B.5) и подставим туда решение (B.30). В результате получим следующее выражение:
(B.31)
Интеграл (B.31) есть не что иное, как разложение начальной волновой функции в интеграл Фурье. Используя обратное преобразование Фурье, находим коэффициенты C (k).
. (B.32)
Резюме . Под свободным движением электрона понимается движение в отсутствии внешнего поля в бесконечной области пространства. Если известна волновая функция электрона в начальный момент времени Y 0 (x), то с помощью формул (B.32) и (B.30) можно найти общее решение уравнения Шредингера Y(x,t) для свободного движения электрона.
В развитие идеи де-Бройля о волновых свойствах вещества Э. Шрёдингер получил в 1926 г. свое знаменитое уравнение. Шрёдингер сопоставил движению микрочастицы комплексную функцию координат и времени, которую он назвал волновой функцией и обозначил греческой буквой «пси» (). Мы будем называть ее пси-функцией.
Пси-функция характеризует состояние микрочастицы. Вид функции получается из решения уравнения Шрёдингера, которое выглядит следующим образом:
Здесь - масса частицы, i - мнимая единица, - оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам:
Буквой U в уравнении (21.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. В случае, когда функция U не зависит явно от времени, она имеет смысл потенциальной энергии частицы.
Из уравнения (21.1) следует, что вид пси-функции определяется функцией U, т. е. в конечном счете характером сил, действующих на частицу.
Уравнение Шрёдингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.
Шрёдингер установил свое уравнение, исходя из оптико-механической аналогии. Эта аналогия заключается в сходстве уравнений, описывающих ход световых лучей, с уравнениями, определяющими траектории частиц в аналитической механике. В оптике ход лучей удовлетворяет принципу Ферма (см. § 115 2-го тома), в механике вид траектории удовлетворяет так называемому принципу наименьшего действия.
Если силовое поле, в котором движется частица, стационарно, то функция V не зависит явно от времени и имеет, как уже отмечалось, смысл потенциальной энергии. В этом случае решение уравнения Шрёдингера распадается на два множителя, один из которых зависит только от координат, другой - только от времени:
Здесь Е - полная энергия частицы, которая в случае стационарного поля остается постоянной. Чтобы убедиться в справедливости выражения (21.3), подставим его в уравнение (21.1). В результате получим соотношение
Сократив на общий множитель придем к дифференциальному уравнению, определяющему функцию
Уравнение (21.4) называется уравнением Шрёдингера для стационарных состояний. В дальнейшем мы будем иметь дело только с этим уравнением и для краткости будем называть его просто уравнением Шрёдингера. Уравнение, (21.4) часто пишут в виде
Поясним, как можно прийти к уравнению Шрёдингера. Для простоты ограничимся одномерным случаем. Рассмотрим свободно движущуюся частицу.
Согласно идее де-Бройля ей нужно сопоставить плоскую волну
(в квантовой механике принято показатель экспоненты брать со знаком минус). Заменив в соответствии с (18.1) и (18.2) через Е и , придем к выражению
Продифференцировав это выражение один раз по t, а второй раз дважды по х, получим
В нерелятивистской классической механике энергия Е и импульс свободной частицы связаны соотношением
Подставив в это соотношение выражения (21.7) для Е и и сократив затем на , получим уравнение
которое совпадает с уравнением (21.1), если в последнем положить
В случае частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U, энергия Е и импульс связаны соотношением
Распространив и на этот случай выражения (21.7) для Е и получим
Умножив это соотношение на , перенеся член влево, придем к уравнению
совпадающему с уравнением (21.1).
Изложенные рассуждения не имеют доказательной силы и не могут рассматриваться как вывод уравнения Шрёдингера. Их цель - пояснить, каким образом можно было прийти к установлению этого уравнения.
В квантовой механике большую роль играет понятие Под оператором подразумевают правило, посредством которого одной функции (обозначим ее ) сопоставляется другая функция (обозначим ее ). Символически это записывается следующим образом:
Здесь - символическое обозначение оператора (с таким же успехом можно было взять любую другую букву с «шляпкой» над ней, например и т. д.). В формуле (21.2) роль Q играет роль - функция F, а роль f - правая часть формулы.
Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как именно она, или, точнее, величина |Ψ| 2 , определяет вероятность пребывания частицы в момент времени t в объеме ΔV, т. е. в области с координатами х и х + dх, у и у + dу, z и z + dz .
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером . Уравнение Шрёдингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы.
Общее уравнение Шредингера имеет вид:
где ? = h /
(2π
), m
- масса частицы, Δ - оператор Лапласа 
, i
- мнимая единица, U
(x, y, z, t
) - потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x, y, z, t
) - искомая волновая функция частицы.
Уравнение (1) справедливо для любой частицы (со спином, равным 0), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью υ «с.
Оно дополняется условиями , накладываемыми на волновую функцию:
1) волновая функция должна быть конечной, однозначной и непрерывной;
2) производные 
должны быть непрерывны;
3) функция |Ψ| 2 должна быть интегрируема (это условие в простейших случаях сводится к условию нормировки вероятностей).
Уравнение (1) называют уравнением Шредингера, зависящим от времени.
Дли многих физических явлений, происходящих в микромире, уравнение (1) можно упростить, исключив зависимость Ψ от времени, т.е. найти уравнение Шредингера для стационарных состояний - состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функция U = U (х, у , z ) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде
. (2)
Уравнение (2) называется уравнением Шредингера для стационарных состояний.
В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций : вол новые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными.
Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями Ψ. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения, которые соответствуют собственным значениям энергии, называются собственнымифункциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором - о дискретном спектре.
Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»
Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
где l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 2).
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:
. (1)
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = 1) непрерывная волновая функция также должна обращаться в нуль.
Следовательно, граничные условия в данном случае имеют вид:
Ψ (0) = Ψ (l ) = 0. (2)
В пределах «ямы» (0 ≤ х ≤ 0) уравнение Шредингера (1) сведется к уравнению:
или 
. (3)
где k 2 = 2mE / ? 2 . (4)
Общее решение дифференциального уравнения (3):
Ψ (x ) = A sin kx + B cos kx .
Так как по (2) Ψ (0) = 0, то В = 0. Тогда
Ψ (x ) = A sin kx . (5)
Условие Ψ (l ) = A sin kl = 0 (2) выполняется только при kl = nπ , где n - целые числа, т.е. необходимо, чтобы
k = nπ / l . (6)
Из выражений (4) и (6) следует, что:
(n
= 1, 2, 3,…), (7)
т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е п, зависящих от целого числа п. Следовательно, энергия Е п частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется.
Квантованные значения энергии Е п называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е п, или, как говорят, частица находится в квантовом состоянии п.
Подставив в (5) значение k из (6), найдем собственные функции:
.
Постоянную интегрирования А найдем из условия нормировки, которое для данного случая запишется в виде:
.
В результате интегрирования получим , а собственные функции будут иметь вид:
(n
= 1, 2, 3,…). (8)
Графики собственных функций (8), соответствующие уровням энергии (7) при n = 1,2,3, приведены на рис. 3, а. На рис. 3, б изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная Ψ n (x ) 2 = Ψ n (x )·Ψ n * (x ) для п = 1, 2 и 3. Из рисунка следует, что, например, в квантовом состоянии с п= 2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.
Из выражения (7) вытекает, что энергетический интервал между двумя соседними уровнями равен:
Например, для электрона при размерах ямы l = 10 -1 м (свободные электроны в металле), ΔЕ n ≈ 10 -35 ·n Дж ≈ 10 -1 6 n эВ, т.е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными (l ≈ 10 -10 м), то для электрона ΔЕ n ≈ 10 -17 n Дж ≈ 10 2 n эВ, т.е. получаются явно дискретные значения энергии (линейчатый спектр).
Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.
Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная π 2 ? 2 /(2т1 2 ). Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Δх частицы в «яме» шириной l равна Δх = l .
Тогда, согласно соотношению неопределенностей, импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса Δр ≈ h / l . Такому разбросу значений импульса соответствует кинетическая энергия Е min ≈ (Δp ) 2 / (2m ) = ? 2 / (2ml 2 ). Все остальные уровни (п > 1) имеют энергию, превышающую это минимальное значение.
Из формул (9) и (7) следует, что при больших квантовых числах (n »1) ΔЕ n / E п ≈ 2/п «1, т. е. соседние уровни расположены тесно: тем теснее, чем больше п. Если п очень велико, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов — дискретность - сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.
Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны - они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики - и с блеском справился с этой задачей.
Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) - в такой передаче энергии участвуют частицы - или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа - корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений - волновыми уравнениями. Все без исключения волны - волны океана, сейсмические волны горных пород, радиоволны из далеких галактик - описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.
Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу - в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное - примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):
где - расстояние, - постоянная Планка , а , и - соответственно масса, полная энергия и потенциальная энергия частицы.
Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.
Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера - Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий - то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.
Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч - это частица, звук - это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле - и эксперименты это вскоре показали - в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).
Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, - яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.
Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания».
Джеймс Трефил - профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.
| Комментарии: 0 |
Макс Планк - один из основоположников квантовой механики - пришел к идеям квантования энергии, пытаясь теоретически объяснить процесс взаимодействия между недавно открытыми электромагнитными волнами и атомами и, тем самым, разрешить проблему излучения черного тела. Он понял, что для объяснения наблюдаемого спектра излучения атомов нужно принять за данность, что атомы излучают и поглощают энергию порциями (которые ученый назвал квантами) и лишь на отдельных волновых частотах.
Абсолютно черное тело, полностью поглощающее электромагнитное излучение любой частоты, при нагревании излучает энергию в виде волн, равномерно распределенных по всему спектру частот.
Слово «квант» происходит от латинского quantum («сколько, как много») и английского quantum («количество, порция, квант»). «Механикой» издавна принято называть науку о движении материи. Соответственно, термин «квантовая механика» означает науку о движении материи порциями (или, выражаясь современным научным языком науку о движении квантующейся материи). Термин «квант» ввел в обиход немецкий физик Макс Планк для описания взаимодействия света с атомами.
Один из фактов субатомного мира заключается в том, что его объекты - такие как электроны или фотоны - совсем не похожи на привычные объекты макромира. Они ведут себя и не как частицы, и не как волны, а как совершенно особые образования, проявляющие и волновые, и корпускулярные свойства в зависимости от обстоятельств. Одно дело - это заявить, и совсем другое - связать воедино волновые и корпускулярные аспекты поведения квантовых частиц, описав их точным уравнением. Именно это и было сделано в соотношении де Бройля.
В повседневной жизни имеется два способа переноса энергии в пространстве - посредством частиц или волн. В обыденной жизни между двумя механизмами передачи энергии видимых противоречий не наблюдается. Так, баскетбольный мяч - это частица, а звук - это волна, и всё ясно. Однако в квантовой механике всё обстоит отнюдь не так просто. Даже из простейших опытов с квантовыми объектами очень скоро становится понятно, что в микромире привычные нам принципы и законы макромира не действуют. Свет, который мы привыкли считать волной, порой ведет себя так, будто состоит из потока частиц (фотонов), а элементарные частицы, такие как электрон или даже массивный протон, нередко проявляют свойства волны.
Больше всего Эйнштейн протестовал против необходимости описывать явления микромира в терминах вероятностей и волновых функций, а не с привычной позиции координат и скоростей частиц. Вот что он имел в виду под «игрой в кости». Он признавал, что описание движения электронов через их скорости и координаты противоречит принципу неопределенности. Но, утверждал Эйнштейн, должны существовать еще какие-то переменные или параметры, с учетом которых квантово-механическая картина микромира вернется на путь целостности и детерминизма. То есть, настаивал он, нам только кажется, будто Бог играет с нами в кости, потому что мы не всё понимаем. Тем самым он первым сформулировал гипотезу скрытой переменной в уравнениях квантовой механики. Она состоит в том, что на самом деле электроны имеют фиксированные координаты и скорость, подобно ньютоновским бильярдным шарам, а принцип неопределенности и вероятностный подход к их определению в рамках квантовой механики - результат неполноты самой теории, из-за чего она и не позволяет их доподлинно определить.
Юлия Зотова
Вы узнаете: Какие технологии называются квантовыми и почему. В чем преимущество квантовых технологий перед классическими. Что может и что не может квантовый компьютер. Как физики делают квантовый компьютер. Когда он будет создан.
Французский физик Пьер Симон Лаплас поставил важный вопрос, о том, всё ли в мире предопределено предыдущим состоянием мира, либо же причина может вызвать несколько следствий. Как и предполагается философской традицией сам Лаплас в своей книге «Изложение системы мира» не задавал никаких вопросов, а сказал уже готовый ответ о том, что да, всё в мире предопределено, однако как часто и случается в философии предложенная Лапласом картина мира не убедила всех и тем самым его ответ породил дискуссию вокруг того вопроса, которая продолжается и по сей день. Несмотря на мнение некоторых философов от том, что квантовая механика разрешила данный вопрос в пользу вероятностного подхода, тем не менее, теория Лапласа о полной предопределенности или как её иначе называют теория лапласовского детерминизма обсуждаема и сегодня.
Гордей Лесовик
Некоторое время назад мы с группой соавторов начали выводить второй закон термодинамики с точки зрения квантовой механики. Например, в одной из его формулировок, гласящей, что энтропия замкнутой системы не убывает, типично растет, а иногда остается постоянной, если система энергетически изолирована. Используя известные результаты квантовой теории информации, мы вывели некоторые условия, при которых это утверждение справедливо. Неожиданно выяснилось, что эти условия не совпадают с условием энергетической изолированности систем.
Профессор физики Джим Аль-Халили исследует наиболее точную и одну из самых запутанных научных теорий - квантовую физику. В начале 20-го века учёные проникли в скрытые глубины материи, в субатомные строительные блоки мира вокруг нас. Они обнаружили явления, которые отличаются от всего увиденного ранее. Мир, где всё может находится во многих местах одновременно, где действительность по-настоящему существует, лишь когда мы наблюдаем за ней. Альберт Эйнштейн противился одной только мысли о том, что в основе сущности природы лежит случайность. Квантовая физика подразумевает, что субатомные частицы могут взаимодействовать быстрее скорости света, а это противоречит его теории относительности.
