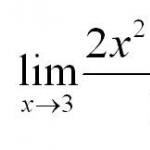Плоские и двугранные углы трехгранного угла. Трёхгранные и многогранные углы: Трёхгранным углом называется фигура образованная тремя плоскостями, ограни- ченными тремя лучами, исходящими из одной

20. Разноуровневое изучение многогранных углов, свойств плоских углов трехгранного угла и многогранного угла.

Базовый уровень:

Атанасян

Рассматривает только Двугранный угол.

Погорелов

Сначала рассматривает двугранный угол и затем сразу трехгранный и многогранный.

Рассмотрим три луча а, b, с, исходящие из одной точки лежащие в одной плоскости. Трехгранным углом (abc) называется фигура, составленная из трех плоских углов (ab), (bc) и (ac) (рис. 400). Эти углы называются гранями трехгранного угла, а их стороны - ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.

Аналогично вводится понятие многогранного угла(рис.401).

рис 400 и рис.401

Профильный уровень (А.Д.Алексндров, А.Л.Вернер, В.И.Рыжих):

Оставляя определение и изучение произвольных многогранных углов до § 31, мы рассмотрим сейчас простейшие из них - трехгранные углы. Если в стереометрии аналогами плоских углов можно считать двугранные углы, то трехгранные углы можно рассматривать как аналоги плоских треугольников , а в следующих параграфах увидим, как они естественно связаны со сферическими треугольниками.

Построить (а значит, и конструктивно определить) трехгранный угол можно так. Возьмем любые три луча а, b,c, имеющие общее начало О и не лежащие в одной плоскости (рис. 150). Эти лучи являются сторонами трех выпуклых плоских углов: угла α со сторонамиb, с, угла β со сторонами а, с и угла γ со сторонами а,b. Объединение этих трех углов α, β, γ и называется трехгранным углом Оabc(или, короче, трехгранным углом О). Лучи а,b, с называются ребрами трехгранного угла Оаbс, а плоские углы α, β, γ - его гранями. Точка О называется вершиной трехгранного угла.

3 а м е ч а н и е. Можно было бы определить трехгранный угол и с невыпуклой гранью (рис. 151), но мы такие трехгранные углы рассматривать не будем.

При каждом из ребер трехгранного угла определяется соответствующий двугранный угол, такой, ребро которого содержит соответствующее ребро трехгранного угла, а грани которого содержат прилежащие к этому ребру грани трехгранного угла.

Величины двугранных углов трехгранного угла Оаbс при ребрах а,b, с будем соответственно обозначать через а^,b^, с^(крышечки непосредственно над буквами).

Три грани α, β, γ трехгранного угла Оаbс и три его двугранных угла при ребрах а,b, с, а также велbчины α, β, γ и а^,b^, с^ будем называть элементами трехгранного угла. (Вспомните, что элементы плоского треугольника - это его стороны и его углы.)

Наша задача - Выразить одни элементы трехгранного угла через другие его элементы, т. е. построить «тригонометрию» трехгранных углов.

1) Начнем с вывода аналога теоремы косинусов. Сначала рассмотрим такой трехгранный угол Оаbс, у которого хотя бы две грани, например α и β являются острыми углами. Возьмем на его ребре с точку С и проведем из нее в гранях α и β перпендикуляры СВ и СА к ребру с до пересечения с ребрами а иbв точках А и В (рис. 152). Выразим расстояние АВ из треугольников ОАВ и САВ по теореме косинусов.

АВ 2 =АС 2 +ВС 2 -2АС*ВС*Cos(c^) и АВ 2 =ОА 2 +ОВ 2 -2АО*ВО*Cosγ.

Вычитая из второго равенства первое, получим:

ОА 2 -АС 2 +ОВ 2 -ВС 2 +2АС*ВС*Cos(c^)-2АО*ВО*Cosγ=0 (1). Т.к. треугольники ОСВ и ОСА прямоугольные, то АС 2 -АС 2 =ОС 2 и ОВ 2 -ВС 2 =ОС 2 (2)

Поэтому из (1) и (2) следует, что ОА*ОВ*Cosγ=ОС 2 +АС*ВС*Cos(c^)

т.е.

Но
,
,
,
. Поэтому

(3) – аналог теоремы косинусов для трехгранных углов-формула косинусов .

Обе грани α и β – тупые углы.

Один из углов α и β, например α, острый, а другой – β- тупой.

Хоты бы 1 из углов α или β прямой.

Признаки равенства трехгранных углов похожи на признаки равенства треугольников. Но есть отличие: например, два трехгранных угла равны, если соответственно равны их двугранные углы. Вспомните, что два плоских треугольника, у которых соответственные углы равны, подобны. А для трехгранных углов аналогичное условие приводит не к подобию, а к равенству.

Трехгранные углы обладают замечательным свойством , которое называется двойственностью. Если в какой-либо теореме о трехгранном угле Оаbс заменить величины а,b, с на π-α, π-β, π-γи, наоборот, заменить α, β, γ на π-a^, π-b^, π-c^, то снова получим верное утверждение о трехгранных углах, двойственное исходной теореме. Правда, если такую замену произвести в теореме синусов, то снова придем к теореме синусов (она сама себе двойственна). Но если так сделать в теореме косинусов (3), то получим новую формулу

cosc^= -cosa^ cosb^+sina^ sin b^ cosγ.

Почему имеет место такая двойственность, станет ясно, если для трехгранного угла построить двойственный ему трехгранный угол, ребра которого перпендикулярны граням исходного угла (см. п. 33.3 и рис. 356).

Одними из простейших поверхностей являются многогранные углы . Они составляются из обычных углов (такие углы теперь часто будем называть плоскими углами), подобно тому как замкнутая ломаная составляется из отрезков. А именно дается следующее определение:

Многогранным углом называется фигура, образованная плоскими углами так, что выполнены условия:

1) Никакие два угла не имеют общих точек, кроме их общей вершины или целой стороны.

2) У каждого из этих углов каждая его сторона является общей с одним и только с одним другим таким углом.

3) От каждого угла к каждому можно перейти по углам, имеющим общие стороны.

4) Никакие два угла с общей стороной не лежат в одной плоскости (рис. 324).

При этом условии плоские углы, образующие многогранный угол, называются его гранями, а их стороны - его ребра.

Под данное определение подходит и двугранный угол. Он составлен из двух развернутых плоских углов. Вершиной его может считаться любая точка на его ребре, и эта точка разбивает ребро на два ребра, сходящиеся в вершине. Но ввиду этой неопределенности в положении вершины двугранный угол исключают из числа многогранных углов.

П

онятие о многогранном угле важно, в частности, при изучении многогранников - в теории многогранников. Строение многогранника характеризуется тем, из каких граней он составлен и как они сходятся в вершинах, т. е. какие там оказываются многогранные углы.

Рассмотрите многогранные углы у разных многогранников.

Обратите внимание, что грани многогранных углов могут быть и невыпуклыми углами.

Аннотация

Цель данного пособия - помочь лицеистам в изучении важной темы курса стереометрии, которая невнятно (или никак не) изложена в стандартных учебниках геометрии. Разобраны определения, основные теоремы и, главное, - методы решения задач, в которых необходимы и естественно используются свойства трехгранных углов.
Трехгранный угол
Определение . Даны плоский многоугольник F и точка S, не принадлежащая плоскости этого многоугольника. Фигура, являющаяся объединением всех лучей с общим началом S и пересекающих F , называется многогранным углом (n -гранным) углом .

S – вершина , лучи SA, SB, SC,… (точки A, B, C,… - вершины многоугольника F ) – ребра , плоскости ASB, BSC,… - грани , углы ASB, BSC,… - плоские углы многогранного угла.

Точка P называется внутренней точкой многогранного угла, если луч SP пересекает внутренность многоугольника F .

Две грани, имеющие общее ребро, образуют двугранный угол многогранного угла.

Если F – выпуклый многоугольник, соответствующий многогранный угол называется выпуклым .

Обозначение : SABC… (A, B, C, … - точки последовательных ребер, то есть вершины многоугольника, являющегося пересечением многогранного угла плоскостью, пересекающей все ребра угла).

При n=3 получаем трехгранный угол – основной для нас объект изучения. Величины трех плоских и трех двугранных углов – основные параметры трехгранного угла.

Задача 1 . В трехгранном угле, все плоские углы которого прямые, двугранные углы также прямые. Докажите.

Решение . Куб и его вершина!
Замечание . Обратное утверждение к задаче 1 тоже верно, но прямое доказательство не так просто. К этому полезно вернуться после формулировки теоремы косинусов для трехгранного угла.
Задача 2 . Все плоские углы трехгранного угла прямые. Найдите угол между биссектрисами двух плоских углов.

Решение . То же самое, что в задаче 1: если на ребрах трехгранного угла в его вершине S построить куб, то диагонали смежных граней куба, пересекающиеся в вершине S, окажутся как раз нужными биссектрисами. Ответ .
.
Задача 3 . Через точку ребра, удаленную на 12 см от вершины трехгранного угла, все плоские углы которого равны
, проведена плоскость, перпендикулярная биссектрисе плоского угла противоположной грани. Найдите отрезки, отсекаемые этой плоскостью от других ребер трехгранного угла.

Решение . Отложим на всех ребрах отрезки SA = SB = SC = 12 см – получим правильный тетраэдр SABC (все боковые грани – правильные треугольники). Данная плоскость, проходящая через точку A, отсекает от биссектрисы (медианы) противоположной грани 2/3 ее длины. Ответ . 8 см.
Задача 4
, а два других – по
. Через произвольную точку A ребра, противолежащего большему из плоских углов, проведена плоскость, перпендикулярная биссектрисе этого плоского угла и пересекающая другие ребра в точках B и C. Найдите: а) угол ABC; б) угол между плоскостью прямого угла и противолежащим ему ребром.

Решение . Точка A проектируется в точку биссектрисы (теорема 4 – см. ниже).

Ответ . а)
; б)
.
Задача 5 . Один из плоских углов трехгранного угла равен
, а два других – по
. Из произвольной точки ребра, противолежащего плоскому углу в
, опущены перпендикуляры на два других ребра. Найдите угол между этими перпендикулярами.

Решение .

, AS = a,
,
,
, BS=CS (из равенства прямоугольных треугольников ABS и ACS по гипотенузе и острому углу); D – середина BC,

Ответ .
.

Теорема 1 . В трехгранном угле каждый плоский угол меньше суммы двух других плоских углов и больше их разности.

Доказательство .

Пусть
– наибольший из плоских углов трехгранного угла SABC . В плоскости ASC построим
луч SD лежит внутри угла ASC (или точки D и C совпадают). Возьмем SB = SD и проведем прямую ADC . В треугольнике ABC: AD + DC AB + BC (даже если DC =0 ) – это неравенство треугольника. . Теперь рассмотрим треугольники CSD и CSB: SD = SB , SC = SC , DC BC , следовательно, ,т.е. . .

Теорема 2. Сумма плоских углов трехгранного угла меньше

Доказательство . Тот же чертеж, что в теореме 1: применим теорему 1 к каждому из трехгранных углов с вершинами A, B, C ( и т.д.) и сложим почленно полученные 9 неравенств; после очевидных сокращений придем куда надо.
Теорема 3. Сумма плоских углов выпуклого многогранного угла меньше
.

Доказательство можно прочитать, например, в учебнике Киселева.
Теорема 4 . Если в трехгранном угле два плоских угла равны, проекцией ребра, являющегося общей стороной равных углов, на плоскость противолежащей грани является биссектриса плоского угла (или ее продолжение) этой грани.

Доказательство . Очевидно.
Задача 6
. Докажите, что если сечение этого угла плоскостью, перпендикулярной к грани с наибольшим плоским углом, имеет форму равнобедренного треугольника (его основание лежит в плоскости прямого угла), то секущая плоскость отсекает на ребрах трехгранного угла равные отрезки.

Решение .
если
, то
; BD=DC (т.к. BA=CA по условию); треугольник BSC – прямоугольный, поэтому D – центр описанной окружности, значит DC=DB=DS (ортогональные проекции AC, AB, AS на плоскость BSC); отсюда следует равенство наклонных: AC=AB=AS; следовательно, треугольники ASB и ASC – правильные () и SA=SB=SC.
Задача 7 . Докажите утверждение, обратное к высказанному в предыдущей задаче.

Решение . Рассуждения в решении задачи 6 нужно обратить (т.к. утверждение задачи 7 является обратным к утверждению предыдущей).
Задача 8 . Плоские углы трехгранного угла равны
. Найдите углы наклона ребер к плоскостям противоположных граней.

Решение . См. чертеж к задаче 6. SA=SB=SC=a, .

Проектируем ортогонально BS на плоскость ASC: пусть
; перпендикуляр из точки K в треугольнике ASC проходит через точку C; искомая проекция E точки B – основание высоты BE в треугольнике BCK!

(теорема косинусов); .
.

Ответ .
.

Теорема 5 (теорема косинусов для трехгранного угла). Пусть
– плоские углы трехгранного угла, A, B, C - противолежащие им двугранные углы. Тогда .

Доказательство . Пусть SA = a. Тогда
. Выразим BC 2 по теореме косинусов из треугольников BSC и BAC и приравняем полученные выражения; после шаблонных преобразований получим что надо.
Задача 9 . Все плоские углы трехгранного угла равны, его двугранный угол равен . Найдите косинус плоского угла.

Решение . Теорема косинусов.

Ответ .

Задача 10 . Каждый плоский угол трехгранного угла равен . На одном из ребер взята точка, удаленная от вершины на расстояние a. Найдите расстояние от этой точки до плоскости противолежащей грани.

Решение . AS=a, ,

,
(теорема косинусов),
.
Ответ .
.
Задача 11 . Два плоских угла трехгранного угла равны , третий плоский угол прямой. На общей стороне равных плоских углов взята точка на расстоянии h от плоскости противолежащей грани. Найдите расстояние от этой точки до вершины трехгранного угла.

Решение .

S
A=x, AO=h,
,

(теорема косинусов).

Ответ .
.
Задача 12 . В трехгранном угле два двугранных угла равны по
, их общий плоский угол прямой. Найдите третий двугранный угол.

Решение . ,

Ответ .
.
Теорема 6 (важная). Если два плоских угла трехгранного угла равны, то их общее ребро проектируется на биссектрису (или ее продолжение) плоского угла противоположной грани.

Доказательство . Если дополнить чертеж к задаче 11 перпендикуляром из A на SC, то сразу увидим, что прямоугольные треугольники ASB и ASC равны по гипотенузе и острому углу, поэтому наклонные AB и AC к грани BSC равны, откуда заключаем равенство их проекций OB и OC. Точка O равноудалена от SB и SC, следовательно, лежит на биссектрисе угла BSC (или ее продолжении).
Дополнение к теме “Трехгранный угол”
Задача 13 . Плоские углы трехгранного угла равны
. Найдите угол между биссектрисой угла и противолежащим ему ребром.

Решение .
- единичные векторы, SD – биссектриса угла . Тогда
.

Ответ .
.
Задача 14 (вторая теорема косинусов для трехгранного угла). Докажите, что

Доказательство . Опустим из внутренней точки трехгранного угла перпендикуляры на грани трехгранного угла – получим новый (двойственный или полярный к данному) трехгранный угол с плоскими углами
и двугранными
. Применим 1-ю теорему косинусов.
Задача 15 . Двугранные углы трехгранного угла равны
. Найдите его плоские углы.

Решение . См. задачу 14.

Ответ .
.
Задача 16 . Докажите, что сумма двугранных углов трехгранного угла больше
, но меньше
.

Решение . Построим полярный угол (см. задачу 14) и применим теорему 2.
Задача 17 (теорема синусов для трехгранного угла). В трехгранном угле

Доказательство . Теорема 5.
Серия пособий А.И. Маринина включает также брошюры:
Геометрия-10 (теория)

Задачи по геометрии-10

Фигура, образованная тремя лучами, исходящими из одной точки О и не лежащими в одной плоскости, и тремя частями плоскостей, заключенных между этими лучами, называется трехгранным углом (рис. 352).

Точка О называется вершиной угла, лучи а, b, с - его ребрами, части плоскостей . Грани суть плоские углы, называемые также плоскими углами данного трехгранного угла. Углы между плоскими гранями называются двугранными углами данного трехгранного угла.

Теорема 1. В трехгранном угле каждый плоский угол меньше суммы двух других.

Доказательство. Достаточно доказать теорему для наибольшего из плоских углов. Пусть наибольший плоский угол трехгранного угла на рис. 353. Построим в плоскости угол , равный углу его сторона b пройдет внутри угла угол наибольший из плоских углов!).

Отложим на прямых с и b какие-либо равные отрезки Проведем через точки произвольную плоскость, пересекающую лучи а и b в точках N и М соответственно.

Треугольники равны, как имеющие равные углы, заключенные между равными сторонами. Покажем, что угол с вершиной О в больше угла с той же вершиной в . Действительно, эти углы заключены между парами равных сторон, третья же сторона больше в треугольнике

Отсюда видно, что сумма двух плоских углов больше третьего плоского угла что и требовалось доказать.

Теорема 2. Сумма плоских углов трехгранного угла меньше четыре прямых.

Доказательство. Возьмем три точки А, В и С на ребрах трехгранного угла и проведем через них секущую плоскость, как показано на рис. 354. Сумма углов треугольника ABC равна Следовательно, сумма шести углов ОАС, ОАВ, ОСА, ОСВ, ОВС, ОВА больше, чем как по предыдуще теореме . Но сумма углов трех треугольников ОАВ, ОВС, ОСА в гранях трехгранного угла равна . Таким образом, на долю плоских углов трехгранного угла остается меньше четырех прямых: . Эта сумма может быть сколь угодно малой («трехгранный шпиль») или сколь угодно близкой к если уменьшать высоту пирамиды SABC на рис. 355, сохраняя ее основание, то сумма плоских углов при вершине S будет стремиться к

Сумма двугранных углов трехгранного угла также имеет границы. Ясно, что каждый из двугранных углов и потому сумма их менее . Для той же пирамиды на рис. 355 эта сумма по мере уменьшения высоты пирамиды приближается к своей границе Можно также показать, что сумма эта всегда хотя может отличаться от сколь угодно мало.

Таким образом, для плоских и двугранных углов трехгранного угла имеют место неравенства

Имеется существенное сходство между геометрией треугольника на плоскости и геометрией трехгранного угла. При этом можно проводить аналогию между углами треугольника и двугранными углами трехгранного угла, с одной стороны, и между сторонами треугольника и плоскими углами трехгранного угла - с другой. Например, при указанной замене понятий сохраняют силу теоремы о равенстве треугольников. Приведем соответствующие формулировки параллельно:

Однако два трехгранных угла, у которых равны соответственные двугранные углы, равны между собой. Между тем два треугольника, углы которых соответственно равны, подобны, но не обязательно равны. Для трехгранных углов, как и для треугольников, ставится задача решения трехгранного угла, т. е. задача отыскания одних его элементов по другим заданным. Приведем пример подобной задачи.

Задача. Даны плоские углы трехгранного угла. Найти его двугранные углы.

Решение. Отложим на ребре а отрезок и проведем нормальное сечение ABC двугранного угла а. Из прямоугольного треугольника ОАВ находим Также имеем

Для ВС находим по теореме косинусов примененной к треугольнику ВАС (для краткости плоские углы обозначаем просто ab, ас, bс, двугранные - а, b, с)

Теперь применим теорему косинусов к треугольнику ВОС:

Отсюда находим

и аналогично

По этим формулам можно найти двугранные углы, зная плоские углы. Отметим еще без доказательства замечательное соотношение

называемое теоремой синусов.

Объяснение глубокой аналогии между геометрией трехгранного угла и геометрией треугольника нетрудно получить, если провести следующее построение. Поместим в вершину трехгранного угла О центр сферы единичного радиуса (рис. 357).

Тогда ребра пересекут поверхность сферы втрехточках А, В, С, грани угла высекут на сфере дуги больших кругов АС, АВ, ВС. На сфере образуется фигура ABC, называемая сферическим треугольником. Дуги («стороны» треугольника) измеряются плоскими углами трехгранного угла, углы при вершинах суть плоские углы двугранных углов. Поэтому решение трехгранных углов есть не что иное, как решение сферических треугольников, которое составляет предмет сферической тригонометрии. Соотношения (243.1) и (243.2) относятся к числу основных соотношений сферической тригонометрии. Сферическая тригонометрия имеет важное значение для астрономии. Таким образом, теория трехгранных углов есть теория сферических треугольников и потому во многом сходна с теорией треугольника на плоскости. Различие этих теорий состоит в том, что: 1) у сферического треугольника и углы и стороны измеряются в угловой мере, поэтому, напрнмер, в теореме синусов фигурируют не стороны, а синусы сторон АВ, АС, ВС;

Глава IV. Прямые и плоскости в пространстве. Многогранники

§ 56. Трехгранные и многогранные углы

Пусть даны /\ АВС и точка S, не принадлежащая плоскости треугольника (рис. 168).
Объединение всех лучей, имеющих общее начало в точке S и пересекающих данный треугольник (рис. 169), называется трехгранным углом .

Точка S называется вершиной трехгранного угла, лучи SA, SB, SC - его ребрами . Углы ASB, BSC, CSA называются гранями трехгранного угла или его плоскими углами . Величина каждого из них принадлежит интервалу ]0°; 180°[.

Вообще, если даны многоугольник ABC ... N и точка S, не принадлежащая плоскости многоугольника, то объединение всех лучей, имеющих общее начало в точке S и пересекающих данный многоугольник (рис. 170), называется многогранным углом .

Точка S называется вершиной многогранного угла, лучи SA, SB, SN - его ребрами. Углы ASB, BSC, ... называются гранями многогранного угла или его плоскими углами ; величина каждого его плоского угла принадлежит интервалу ]0°; 180°[. Многогранные углы называются трехгранными, четырехгранными и т. д. в зависимости от числа граней. Обозначают многогранный угол или одной буквой, обозначающей вершину, или несколькими буквами, отмечая вершину и точки на каждом ребре.

Многогранный угол называется выпуклым, если он находится по одну сторону от плоскости каждой его грани. В противном случае многогранный угол называется невыпуклым. На рис. 171 изображен невыпуклый пятигранный угол.

Выпуклый многогранный угол называется правильным , если все его грани конгруэнтны и все его двугранные углы конгруэнтны.

Рассмотрим свойства плоских углов трехгранных и многогранных углов.

Теорема 1. Величина каждого плоского угла трехгранного угла меньше суммы величин двух других его плоских углов.

Пусть дан трехгранный угол SABC. Величины его плоских углов обозначим α , β , γ
(рис. 172).

Пусть γ - большая из них. Достаточно доказать, что γ < α + β.

В плоскости грани ASB проведем луч SM так, чтобы . Пусть N - точка пересечения отрезка АВ и луча SM. На луче SC отложим отрезок SD такой, что
|SD| = |SN|. Тогда /\ ASD /\ ASN по двум сторонам и углу между ними.

В /\ ABD

|AD| + |DB| > |AB|,

а по построению

|AB| = |AN| + |NB| и |AD| = |AN|,

следовательно, |DB| > |NB|.

Выразим теперь |DB| и |BN| из треугольников BSD и BSN при помощи теоремы косинусов:

|BD| 2 = |BS| 2 + |DS| 2 - 2|BS| |DS| cos α,
|ВN| 2 = | BS| 2 + |NS| 2 - 2|BS| |NS| cos .

Так как |DS| = |NS| , а | DB |> |NB|, то cos α < cos , и поэтому < α. Тогда

< α + β, или γ < α + β.

Из доказанной теоремы непосредственно следует, что величина каждого плоского угла трехгранного угла больше разности величин двух других его плоских углов, например

α > γ - β, β > γ - α

Теорема 2. Сумма величин всех трех плоских углов трехгранного угла меньше 360° .

Пусть дан трехгранный угол SABC (рис. 173).

Если через точки А, В, С проведем плоскость, то получим еще три трехгранных угла: ASBC, BSAC и CSAB. Применим к каждому из них теорему о сумме величин двух плоских углов трехгранного угла: