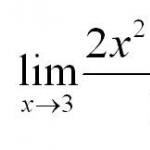(хотя чаще всего совпадает).
Энциклопедичный YouTube
-
1 / 5
Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом :
r → c = ∑ i m i r → i ∑ i m i , {\displaystyle {\vec {r}}_{c}={\frac {\sum \limits _{i}m_{i}{\vec {r}}_{i}}{\sum \limits _{i}m_{i}}},}где r → c {\displaystyle {\vec {r}}_{c}} - радиус-вектор центра масс, r → i {\displaystyle {\vec {r}}_{i}} - радиус-вектор i -й точки системы, m i {\displaystyle m_{i}} - масса i -й точки.
Для случая непрерывного распределения масс:
r → c = 1 M ∫ V ρ (r →) r → d V , {\displaystyle {\vec {r}}_{c}={1 \over M}\int \limits _{V}\rho ({\vec {r}}){\vec {r}}dV,} M = ∫ V ρ (r →) d V , {\displaystyle M=\int \limits _{V}\rho ({\vec {r}})dV,}где M {\displaystyle M} - суммарная масса системы, V {\displaystyle V} - объём, ρ {\displaystyle \rho } - плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.
Можно показать, что если система состоит не из материальных точек, а из протяжённых тел с массами M i {\displaystyle M_{i}} , то радиус-вектор центра масс такой системы R c {\displaystyle R_{c}} связан с радиус-векторами центров масс тел R c i {\displaystyle R_{ci}} соотношением :
R → c = ∑ i M i R → c i ∑ i M i . {\displaystyle {\vec {R}}_{c}={\frac {\sum \limits _{i}M_{i}{\vec {R}}_{ci}}{\sum \limits _{i}M_{i}}}.}Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.
Центры масс плоских однородных фигур
Координаты центра масс однородной плоской фигуры можно вычислить по формулам (следствие из теорем Паппа - Гульдина):
x s = V y 2 π S {\displaystyle x_{s}={\frac {V_{y}}{2\pi S}}} и y s = V x 2 π S {\displaystyle y_{s}={\frac {V_{x}}{2\pi S}}} , где V x , V y {\displaystyle V_{x},V_{y}} - объём тела, полученного вращением фигуры вокруг соответствующей оси, S {\displaystyle S} - площадь фигуры.Центры масс периметров однородных фигур
Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лифшица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (англ. center-of-mass ): оба термина эквивалентны.
Скорость центра масс в релятивистской механике можно найти по формуле:
v → c = c 2 ∑ i E i ⋅ ∑ i p → i . {\displaystyle {\vec {v}}_{c}={\frac {c^{2}}{\sum \limits _{i}E_{i}}}\cdot \sum \limits _{i}{\vec {p}}_{i}.} вес массы P = m·g зависит от параметра гравитационного поля g ), и, вообще говоря, даже расположен вне стержня.В однородном гравитационном поле центр тяжести всегда совпадает с центром масс. В некосмических задачах гравитационное поле обычно может считаться постоянным в пределах объёма тела, поэтому на практике эти два центра почти совпадают.
По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (поскольку реального гравитационного поля нет, то и учёт его неоднородности не имеет смысла). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.
Центром тяжести (или центром масс ) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта . Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач :
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.
В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:

Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:

и, выражая отсюда , мы и получаем требуемую формулу.
Центр масс каркаса
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:

где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.
Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид , т.е. точка, образованная средним арифметическим координат вершин:

Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian "Finding Centroids the Easy Way".
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:

Четыре получившихся треугольника подобны треугольнику с коэффициентом .
Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :

Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):

Наша цель — показать, что вектора и коллинеарны.
Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .
Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):

Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:

откуда находим:
Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .
Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника . Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:

где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .
Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников , поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:

где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).
Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом . Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:

(это можно вывести из того факта, что центроид делит медианы в отношении )
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Снова рассмотрим ту же систему материальных точек. Построим радиус-вектор по следующему правилу:

где - радиус-вектор - той материальной точки системы, а - ее масса.
Радиус-вектор определяет положение в пространстве центра инерции (центра масс) системы.
Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка.
Пример. Найдем центр масс системы, состоящей из двух маленьких шариков - материальных точек, соединенных невесомым стержнем (рис. 3.29). Такая система тел называется гантелей.

Рис. 3.29. Центр масс гантели
Из рис. видно, что


Подставляя в эти равенства выражение для радиус-вектора центра масс



Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l 1 и l 2 между шарами и центром масс равны соответственно


Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:
Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части:

В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс системы. В знаменателе стоит полная масса системы

Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:

Видео 3.11. Движение центра масс двух одинаковых тележек, связанных пружиной.
Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется.
Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:

Видно, что
Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе.
Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы.
Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс ), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе.
В случае, когда системой является тело с непрерывным распределением масс, определение центра масс остается по существу тем же. Окружаем произвольную точку в нашем теле небольшим объемом . Масса, заключенная в этом объеме, равна , где - плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему тела, так что для положения центра масс тела получается выражение

Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид

где - объем тела.
И в случае непрерывного распределения масс справедливо утверждение, что
Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу.
Пример . Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе.
Урок «Центр масс»
Регламент: 2 урока
Цель: Познакомить учащихся с понятием «центр масс» и его свойствами.
Оборудование: фигуры из картона или фанеры, «неваляшка», перочинный нож, карандаши.
План урока
Этапы урока время методы и приемы
I Введение учащихся 10 фронтальный опрос, работа учащихся у доски.
в проблему урока
II. Изучение нового 15-20 Рассказ учителя, решение задачи,
материала: 10 экспериментальное задание
III Отработка нового 10 сообщения учащихся
материала: 10-15 решение задач,
15 фронтальный опрос
IV.Выводы. Домашнее 5-10 Устное обобщение материала учителем.
задание Запись на доске
Ход урока.
I Повторение 1. Фронтальный опрос: плечо силы, момент силы, условие равновесия, виды равновесия
Эпиграф: Центром тяжести каждого тела является некоторая располо-женная внутри его точка - такая, что если за нее мысленно подвесить тело, то оно остается в покое и сохраняет первона-чальное положение.
II . Объяснение нового материала
Пусть дано тело или система тел. Мысленно разобьем тело на сколь угодно малые части с массами m1, m2, m3… Каждую из этих частей можно рассматривать как материальную точку. Положение в пространстве i-ой материальной точки с массой mi определяется радиус-вектором r i (рис. 1.1). Масса тела есть сумма масс отдельных его частей: т = ∑ mi.
Центром масс тела (системы тел) называет-ся такая точка С, радиус-вектор которой определяется по формуле
r = 1/m∙∑ mi r i
Можно показать, что положение центра масс относительно тела не за-висит от выбора начала координат О, т.е. данное выше определение центра масс однозначно и корректно.
Центр масс однородных симметричных тел рас-положен в их геометрическом центре или на оси симметрии, центр масс у плоского тела в виде произвольного треугольника находится на пересече-нии его медиан.
Решение задачи
ЗАДАЧА 1. На легком стержне (рис. 1.2) закреплены однородные ша-ры массами m1 = 3 кг, m2 = 2 кг, m3 = 6 кг, и m4 = 3 кг. Расстояние между центрами любых ближайших шаров
а = 10 см. Найти положе-ние центра тяжести и центра масс конструкции.
РЕШЕНИЕ. Положение относительно шаров центра тяжести конструкции не зависит от ориентации стержня в пространстве. Для ре-шения задачи удобно располо-жить стержень горизонтально, как показано на рисунке 2. Пусть центр тяжести находится на стержне на расстоянии L от центра левого шара, т.е. от т. А. В центре тяжести приложена равнодействующая всех сил тяжести и ее момент относительно оси А равен сумме моментов сил тяжести шаров. Имеем r = (m1 + m2 + m3 + m4) g ,
R L = m2gα + m 3 g 2 а + m 4 g 3 а.
Отсюда L=α (m1 +2m3 + 3m4)/ (m1 + m2 + m3 + m4) ≈ 16,4 см
ОТВЕТ. Центр тяжести совпадает с центром масс и находится, в точке С на расстоянии L=16,4см от центра левого шара.
Оказывается, что у центра масс тела (или системы тел) есть ряд за-мечательных свойств. В динамике показывается, что импульс произвольно движущегося тела равен произведению массы тела на скорость его центра масс и что центр масс движется так, как если бы все внешние силы, действующие на тело, были приложены в центре масс, а масса все-го тела была сосредоточена в нем.
Центром тяжести тела, находящегося в поле тяготения Земли, на-зывают точку приложения равнодействующей всех сил тяжести, дейст-вующих на все части тела. Эта равнодействующая называется силой тя-жести, действующей на тело. Сила тяжести, приложенная в центре тя-жести тела, оказывает на тело такое же воздействие, как и нее силы тя-жести, действующие на отдельные части тела.
Интересен случай, когда размеры тела намного меньше размеров Зем-ли. Тогда можно считать, что на все части тела действуют параллельные силы тяжести, т.е. тело находится в однородном поле тяжести. У парал-лельных и одинаково направленных сил всегда есть равнодействующая, что можно доказать. Но при определенном положении тела в простран-стве можно указать только линию действия равнодействующей всех параллельных сил тяжести, точка ее приложения останется пока неопреде-ленной, т.к. для твердого тела любую силу можно переносить вдоль ли-нии ее действия. Как же быть с точкой приложения?
Можно показать, что при любом положении тела в однородном поле тяжести, линия действия равнодействующей всех сил тяжести, действу-ющих на отдельные части тела, проходят через одну и ту же точку, не-подвижную относительно тела. В этой точке и прикладывается равно-действующая, а сама точка будет центром тяжести тела.
Положение центра тяжести относительно тела зависит только от фор-мы тела и распределения массы в теле и не зависит от положения тела в однородном поле тяжести. Центр тяжести не обязательно находится в са-мом теле. Например, у обруча в однородном поле тяжести центр тяжести лежит в его геометрическом центре.
В однородном поле тяжести центр тяжести те-ла совпадает с его центром масс.
В подавляющем боль-шинстве случаев один термин безбо-лезненно можно заменять другим.
Но: центр масс тела су-ществует независимо от наличия поля тяжести, а о центре тяжести мож-но говорить только при наличии силы тяжести.
Местоположение центра тяжести тела, а значит и центра масс, удобно находить, учитывая симметричность тела и используя понятие момента силы.
Если плечо силы равно нулю, то момент силы равен нулю и такая сила не вызывает вращательного движения тела.
Следовательно, если линия действия силы проходит через центр масс, то оно движется поступательно.
Таким образом, можно определить центр масс любой плоской фигуры. Для этого надо закрепить ее в одной точке, дав ей возможность свободно поворачиваться. Она установится так, чтобы сила тяжести, поворачивающая ее, проходила через центр масс. В точке закрепления фигуры подвесим нить с грузом (гайкой), проведем линию вдоль подвеса (т.е. линию действия силы тяжести). Повторим действия, закрепив фигуру в другой точке. Пересечение линий действия сил тяжести - центр масс тела
Экспериментальное задание: определить центр тяжести плоской фигуры (по приготовленным ранее учащимися фигурам из картона или фанеры).
Инструкция: закрепляем фигурку на штативе. Подвешиваем за один из углов фигуры отвес. Проводим линию действия силы тяжести. Поворачиваем фигуру, повторяем действие. Центр масс лежит в точке пересечения линий действия силы тяжести.
Быстро справившимся с заданием учащимся можно дать дополнительное задание: прикрепить к фигуре груз (металлический болт) и определить новое положение центра масс. Сделать вывод.
Изучение замечательных свойств «центров», которому более двух тыся-челетий, оказалось полезным не толь-ко для механики - например, при конструировании транспортных средств и военной техники, расчете устойчивости сооружений или для вывода уравнений движения реактив-ных аппаратов. Вряд ли Архимед мог даже помыслить о том, что поня-тие центра масс окажется весьма удоб-ным для исследований в ядерной фи-зике или в физике элементарных час-тиц.
Сообщения учащихся:
В своем труде «О равновесии плос-ких тел» Архимед употреблял понятие центра тяжести, фактически не опре-деляя его. Видимо, оно впервые было введено неизвестным предшественни-ком Архимеда или же им самим, но в более ранней, не дошедшей до нас работе.
Должно было пройти долгих сем-надцать столетий, прежде чем наука прибавила к исследованиям Архимеда о центрах тяжести новые результаты. Это произошло, когда Леонардо да Винчи сумел найти центр тяжести тет-раэдра. Он же, размышляя об устойчи-вости итальянских наклонных башен, в том числе - Пизанской, пришел к «теореме об опорном многоугольни-ке».
Выясненные еще Архимедом усло-вия равновесия плавающих тел впос-ледствии пришлось переоткрывать. Занимался этим в конце XVI века: голландский ученый Симон Стевин, применявший, наряду с понятием цен-тра тяжести, и понятие «центр давле-ния» - точку приложения силы давле-ния окружающей тело воды.
Прин-цип Торричелли (а его имя носят и формулы для расчета центра масс), оказывается, был предвосхищен его учителем Галилеем. В свою очередь, этот принцип лег в основу классичес-кого труда Гюйгенса о маятниковых часах, а также был использован в знаменитых гидростатических иссле-дованиях Паскаля.
Метод, позволивший Эйлеру изу-чать движение твердого тела под дей-ствием любых сил, состоял в разложе-нии этого движения на перемещение центра масс тела и вращение вокруг проходящих через него осей.
Для сохранения в неизменном по-ложении предметов при движении их опоры уже несколько столетий приме-няется так называемый карданов под-вес - устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. Примером может служить корабельная керосиновая лампа.
Хотя на Луне сила тяжести в шесть раз меньше, чем на Земле, увеличить там рекорд по прыжкам в высоту уда-лось бы «всего» лишь в четыре раза. К такому выводу приводят расчеты по изменению высоты центра тяжести тела спортсмена.
Помимо суточного вращения вок-руг своей оси и годового обращения вокруг Солнца, Земля принимает уча-стие еще в одном круговом движении. Вместе с Луной она «крутится» вокруг общего центра масс, расположенного примерно в 4700 километрах от центра Земли.
Некоторые искусственные спутни-ки Земли снабжены складной штангой в несколько или даже в десятки мет-ров, утяжеленной на конце (так назы-ваемый гравитационный стабилиза-тор). Дело в том, что спутник вытяну-той формы стремится при движении по орбите повернуться вокруг своего центра масс так, чтобы его продольная ось расположилась вертикально. Тог-да он, подобно Луне, будет все время обращен к Земле одной стороной.
Наблюдения за движением неко-торых видимых звезд свидетельству-ют о том, что они входят в двойные системы, в которых происходит вра-щение «небесных партнеров» вокруг общего центра масс. Одним из невиди-мых компаньонов в такой системе мо-жет быть нейтронная звезда или, воз-можно, черная дыра.
Объяснение учителя
Теорема о центре масс: центр масс те-ла может изменить свое положение только под действием внешних сил.
Следствие теоремы о центре масс: центр масс замкнутой системы тел остается неподвижным при любых взаимодействиях тел системы.
Решение задачи (у доски)
ЗАДАЧА 2. Лодка стоит неподвижно в стоячей воде. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние h сдви-нется лодка, если масса человека m= 60кг, масса лодки М = 120кг, длина лодки L=3м? Сопротивлением воды пренебречь.
РЕШЕНИЕ. Воспользуемся условием задачи, что начальная скорость центра масс равна нулю (лодка и человек вначале покоились) и сопротивление воды отсутствует (никакие внешние силы в горизонтальном направлении на систему «человек-лодка» не действуют). Следователь-но, координата центра масс системы в горизонтальном направлении не изменилась. На рис.3 изображено начальное и конечное положение лодки и человека. Начальная координата х0 центра масс х0 = (mL+ML/2)/(m+M)
Конечная координата х центра масс х = (mh+M(h+L/2))/(m+M)
Приравнивая х0 = х, находим h= mL/(m+M) =1м
Дополнительно: сборник задач Степановой Г.Н. №393
Объяснение учителя
Вспоминая условия равновесия, мы выяснили, что
Для тел, имеющих площадь опоры, устойчивое равновесие наблюдается в том случае, когда линия действия силы тяжести проходит через основание.
Следствие: чем больше площадь опоры и ниже центр тяжести, тем устойчивее положение равновесия.
Демонстрация
Поставьте детскую игрушку неваляш-ку (Ваньку - Встаньку) на шерохова-тую доску и приподнимите правый край доски. В какую сторону откло-нится «голова» игрушки при сохране-нии ее равновесия?
Объяснение: Центр тяжести С неваляшки находится ниже геометрического центра О шарообразной поверхности «туловища». В положе-нии равновесия точка С и точка касания А игрушки с на-клонной плоскостью должны находиться на одной вертикали; следовательно «голова» неваляшки отклонится влево
Как объяснить сохранение рав-новесия в случае, показанном на ри-сунке?
Объяснение: Центр тяжести системы карандаш - нож лежит ниже точ-ки опоры
III Закрепление. Фронтальный опрос
Вопросы и задачи
1. При перемещении тела с экватора на полюс действующая на него сила тяжести меняется. Отражается ли это на положении центра тяжести тела?
Ответ: нет, т.к. относительные изменения силы тяжести всех элементов тела одинаковы.
2. Можно ли найти центр тяжести «гантели», состоящей из двух массив-ных шариков, соединенных невесо-мым стержнем, при условии, что дли-на «гантели» сравнима с диаметром Земли?
Ответ: нет. Условие существования центра тяжести - однород-ность поля тяготения. В неоднородном гравитационном поле повороты «гантели» вокруг ее центра масс приводят к тому, что линии действия L1 и L2, равнодействующих сил тяжести, приложенных к шарикам, не имеют общей точки
3. Почему при резком торможении автомобиля его передняя часть опус-кается?
Ответ: при торможении на колеса со стороны дороги действует сила трения, создающая вращающий момент вокруг центра масс автомобиля.
4. Где находится центр тяжести буб-лика?
Ответ: в дырке!
5. В цилиндрический стакан понем-ногу наливают воду. Как будет изме-няться положение центра тяжести си-стемы стакан - вода?
Ответ: Центр тяжести системы сначала будет понижаться, а потом - повышаться.
6. Какой длины конец надо отрезать от однородного стержня, чтобы его центр тяжести сместился на ∆ℓ?
Ответ: длиной 2∆ℓ.
7. Однородный стержень согну-ли посередине под прямым углом. Где оказался теперь его центр тяжес-ти?
Ответ: в точке О — середине отрезка О1О2, соединяющего сере-дины участков АВ и ВС стержня
9. Неподвижная космическая ста-ция представляет собой цилиндр. Космонавт начинает круговой обход ста-ции по ее поверхности. Что произойдет со станцией?
Ответ: с танция придет во вращение в противоположную сторо-ну, причем ее центр будет описывать окружность вокруг об-щего с космонавтом центра масс.
11. Почему трудно передвигаться на ходулях?
Ответ: центр тяжести человека на ходулях значительно повыша-ется, а площадь его опоры на землю уменьшается.
12. Когда канатоходцу легче удер-жать равновесие - при обычном пере-движении по канату или при переносе сильно изогнутого коромысла, нагру-женного ведрами с водой?
Ответ: Во втором случае, так как центр масс канатоходца с вед-рами лежит ниже, т.е. ближе к опоре - канату.
IV Домашнее задание: (выполняется желающими - задачи трудные, решившие их получают "5").
*1. Найдите центр тяжести системы шаров, находящихся в вершинах равностороннего невесомого треугольника, изображенного на рисунке
Ответ: центр тяжести лежит на середине биссектрисы угла, в вершине которого находится шар массой 2m
*2. Глубина лунки в доске, в кото-рую вставлен шар, в два раза меньше радиуса шара. При каком угле накло-на доски к горизонту шар выскочит из лунки?
Движение системы кроме действующих сил зависит также от ее суммарной массы и распределения масс. Масса системы (обозначаем М или ) равна арифметической сумме масс всех точек или тел, образующих систему.
распределение масс в системе определяется значениями масс ее точек и их взаимными положениями, т. е. их координатами Однако оказывается, что при решении тех задач динамики, которые мы будем рассматривать, в частности динамики твердого тела, для учета распределения масс достаточно знать не все величины , а некоторые, выражаемые через них суммарные характеристики. Ими являются: координаты центра масс (выражаются через суммы произведений масс точек системы на их координаты), осевые моменты инерции (выражаются через суммы произведений масс точек системы на квадраты их координат) и центробежные моменты инерции (выражаются через суммы произведений масс точек системы и двух из их координат). Эти характеристики мы в данной главе и рассмотрим.
Центр масс. В однородном поле тяжести, для которого g=const, вес любой частицы тела пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы (59) из § 32, определяющие координаты центра тяжести тела, к виду, явно содержащему массу. Для этого положим в названных формулах , после чего, сократив на g, найдем:
В полученные равенства входят теперь массы материальных точек (частиц), образующих тело, и координаты этих точек. Следовательно, положение точки действительно характеризует распределение масс в теле или в любой механической системе, если под понимать соответственно массы и координаты точек системы.
Геометрическая точка С, координаты которой определяются формулами (1), называется центром масс или центром инерции механической системы.
Если положение центра масс определять его радиусом-вектором то из равенств (1) для получается формула

где - радиусы-векторы точек, образующих систему.
Из полученных результатов следует, что для твердого тела, находящегося в однородном поле тяжести, положения центра масс и центра тяжести совпадают. Но в отличие от центра тяжести понятие о центре масс сохраняет свой смысл для тела, находящегося в любом силовом поле (например, в центральном поле тяготения), и, кроме того, как характеристика распределения масс, имеет смысл не только для твердого тела, но и для любой механической системы.